圖

○一度四十三分○五秒即初虧及復圓交周也依此交周復查表得初虧視距度○三分三十三秒而復圓得八分五十三秒因此畫本食圖如乙丁及丙戊兩直線以直角在甲相交指南北東西方乙丁為黃道甲心為太陽居其中
圖
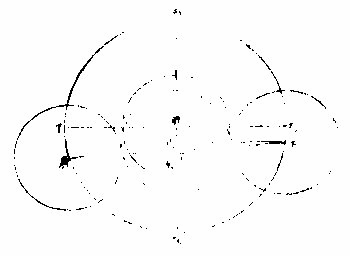
依前食論其太陽半徑得一十五分一十五秒較太陰半徑略小甲戊線則并兩輪半徑為三十二分○五秒因太陰食甚在辛甲辛乃當時視距度○六分一十○秒初虧在壬即乙壬與甲己相等只三分三十三秒復圓在庚得丁庚
與甲癸相等,共八分五十三秒,而壬辛庚皆視距南 也。〈以上原本曆指卷十四交食之六〉
《測食分》第一。〈凡八章。〉
算食而不溯食,將何以攷?其法非強,天即自欺。故必 隨測隨算,了了於目,了了於手,則視差、視徑、時分俱 準,而法乃得矣。
測太陰食分
常法全賴目力。因分太陽徑為一十分,太陰徑亦如 之。食甚時,則以所見不食之徑,約略不能見之餘分, 設并見失光之體,庶幾所食有半者。依此以測猶可, 此外則多有謬焉。何也?太陰未食以前,欲用器測全 徑,食甚時,又測光所存之餘徑,此際甚難。〈其光微又無從定中 線故〉且不正合於法,今補此闕,用太陰地景兩徑之比 例,及太陰見缺之邊。如圖地景心在丙,得乙戊辛弧 為邊,太陰心在甲,以其乙丁辛邊弧入景中為所缺, 自乙至辛作直線,更一直線聯其兩心及兩邊交切 之界於乙或辛為甲乙乙丙及甲丙,而甲丙及乙辛 以直角相交於己,使太陰入景之邊,乙丁辛為六十。
圖

度因半之於丁得乙丁對乙甲己角為三十度必餘角甲乙己為六十度〈甲己乙直角故〉甲、《乙》割線二萬,乙、己止一萬,則以甲乙與乙丙之比例。〈一與三是〉乙丙得六萬,為丙乙己角之割線。查八十度二十四分,本角之切線,五九一二三六為丙己,而
甲己為甲乙己角之切線,一七三二○五兩切線為 甲丁及丙戊所減。〈甲丁與甲乙丙戊與丙乙自相等〉餘丁己二六七 九五,戊己八七六四,并之,得三五五五九,為甲乙二 萬分比例之分。因以推太陰之食分。蓋設太陰半徑, 得一十六分,與之相乘,用二萬除,得食二分五十一 秒。〈度數之分〉即徑分止有五十三秒,以此測雖微有差,所 推徑分終近矣。
測太陽食分
密室中對太陽開小圓孔以受其光。因孔小出光之 體大,則所正照之光必為角形,其底在太陽,其角在 孔之中。夫光一入內,又復展開為角形,以致底所對 之牆轉其原形,以上為下,以左為右,使牆與光直角 相遇,則底為圓形,不則為圓長形。使孔不圓且小,則 光底在牆,或彷彿孔形,而所像太陽之形大都不真。 何也?太陽孔牆三者,皆有遠近大小之比例。蓋孔距 牆得其本徑數,與太陽所距本徑數等,則光底在牆, 必像太陽圓形,及孔之多邊形各等,為雜形。若兩徑 數不等,而太陽距牆得徑數多,則光底失去原形,轉 隨孔形得徑數少,則光底必因之愈少。故測食者恆 設孔小而圓,乃可遠近無差。因以牆「上所缺之形,徵 太陽所食之分。」法。以規器於紙上先畫大小不等數 圓圈,各以徑分之,其徑以十或更密平分之。臨測室 中,以圈受光,不拘遠近,任用大小圈全以脗合於光 為準。既合,便轉紙,使其圈徑橫過餘光形中,平分兩 角,則光缺之界即所食分數。方光與圈合時,遂以筆 於光景間微識三四小點,求心因之作圈,略得太陰 掩太陽大小之比例。如圖甲乙丙丁為太陽食外之
圖

餘光正與甲乙丙圈界相合其心在戊其徑與丁以直角交景而平分甲及丙兩光角則得太陽食七分有奇更取三點為甲丁丙以己為心〈幾何三卷二十四題〉以甲丁丙辛為「太陰」,乃以己丁較戊乙,亦得日月兩徑大小之比例
