欽定古今圖書集成/曆象彙編/曆法典/第061卷

欽定古今圖書集成
曆象彙編 第六十一卷

欽定古今圖書集成曆象彙編曆法典

　第六十一卷目錄

　曆法總部彙考六十一

　　新法曆書十一〈交食曆指三〉

曆法典第六十一卷

曆法總部彙考六十一

《新法曆書》十一。

交食曆指三

《食限》第一。〈凡六章。〉

食限者，日月行兩道，各推其經度，距交若干，為有食 之始也。而日與月不同，月食則太陰與地景相遇，兩 周相切，以其兩視半徑較白道距黃道度，又以距度 推交周度定食限。若日食，則太陽與太陰相遇，雖兩 周相切，其兩視半徑未可定兩道之距度為有視差， 必以之相加而得距度。故特論半徑，則日食之二徑 「狹，月食之二徑廣。」論日食之限，反大於月食之限，以 視差也。

太陰食限

「表中地景半徑最大者，先定四十七分；太陰半徑最 大者，一十七分二十○秒，并得一度○四分二十○ 秒。日月兩道之距」，在此數以內可有月食。〈可食者可不食也〉 以此距度推其相值之交，常得一十二度二十八分， 為月食限。推法最大距度。〈四度五十八分半〉與象限九十度， 若距度與交常之弧也。其最小者，地半景定四十三 分，月半徑一十五分一十五秒，并得五十八分一十 五秒。若距度與之等者，依前法推交常度，得一十一 度一十六分。此限以內，月過景必有食也。〈必食者無不食也〉 抑此兩者，皆論實望時之食限耳，若論平望，其限尤 寬。

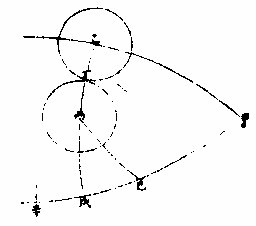
如圖甲乙為黃道，甲丙當白道，乙為地景心，丙為太 陰心月。切景在丁，其最大兩半徑為乙，丙得一度○。

圖

四分二十○秒則相值之甲丙得一十二度二十八分為定望食限設平望尚在前為戊則戊平望距丙定望最遠者二度三十八分有奇為丙戊弧以加甲丙弧得甲戊一十五度○六分有奇為太陰切景之時以其心距兩交之度西

《古史》「《多祿》某，定實望之食限一十二度一十二分，中 望之食限一十五度一十二分，其所定視半徑最小 之食限一十○度五十○分。」

何謂平望？距定望最遠，得二度三十八分，曰太陽均 度最大者二度○三分一十五秒，太陰均度最大者 四度五十八分二十七秒，并得七度○一分四十二 秒，為兩交時日月以實度相距極遠之弧也。從此太 陰逐及於日行訖七度○二分，此時間太陽又自行 三十二分二十八秒，太陰又須逐及更行三十二分。

圖

此時間太陽又行三分弱共為三十五分以加太陽均度得二度三十八分為日月之實會望距其中望也如上圖甲乙為地心所出過本輪心直線至黃道乙指中會太陰實行在丙太陽實行在丁總丙丁弧七度○二分太陰行至丁

太陽已過丁而前又逐及之，終合於己，故《丁己》弧三 十五分加乙丁，共得乙己中實。兩會相距二度三十 八分。

太陽食限

表中太陽之最大半徑一十五分三十○秒，太陰之 最大半徑一十七分二十○秒，并得三十二分五十 ○秒，所謂「二徑折半」也。以此推相值之交，常為六度 四十○分，是太陽不論視差，不分南北，正居實會之 食限也。第日食不在天頂，即有高庳視差，太陰每偏 而在下，交會時以此差故，或就近於太陽，或移遠隨 地隨時，各各不同，安得以實度遽定日食之限乎？測 太陰交食時最大高庳，差得一度○四分

因距遠五十四地半徑故。

減太陽之最大高庳差三分，餘一度○一分。

此為太陰偏南之極多者，凡日食時，必有一方能見其然，是為大地公共之最大差。

以加二徑折半，得總視距度一度三十三分五十○ 秒外，此即無日食，在其內則可食。依前法求食限，得兩交前後各一十八度五十○分，為兩大視徑折半 之限也。若以小半徑求食限，與前差度并，得一度三 十一分有奇，推相值之交周度一十七度四十八分， 為小視徑折半之日食限。若日月會入此限內者，日 必食，但非總大地能見，必有地能見耳。若以中會論 食限，又須加入實會距中會之度，其最大弧三度，則 中會有食之限二十餘度。如圖甲乙為黃道，甲戊為 白道，太陰以實度在己，以視度在丙，太陽乙與太陰 丙視，相切於丁，則己丙為高庳差，己戊為東西差，而

圖

丙戊為南北差南北差之最大者一度○一分以加乙丙為總距度乙戊若乙丙為大折半〈二徑折半省曰折半〉推得甲戊食限，一十八度五十○分。或以小折半，乙丙加丙戊，得甲戊一十七度四十八分。設中會更在前，為辛，得食限，甲辛更多於

甲戊。

求北中界日食限

「北中界」者，地居赤道之北，南不至赤道，北不至北極 也。今依南方極出地十八度，北方極出地四十二度， 定日食之限，則最廣者，太陰距南，其交常度七度三 十一分；太陰距北，其交常度一十七度三十五分，為 可食之限。最狹者，太陰距南交常七度，距北交常一 十六度五十三分，為必食之限。其所繇廣狹者，因二 徑折半，有大有小，即相會時所當距度不同，故所限 交周度亦異也。太陰分南北而定最大日食之限，有 二義：其一，論地總本界中有一方焉，距北之最大者， 以十七度為限。又有一方焉，距南之最大者，以七度 為限。非謂一方所見，距北可得十七，距南又可得七 也。其一，論黃道度，為本界中有地有時。太陰或南或 北，距天頂最遠，則其視距度最大。以加於太陰實距 度，得其最大限。在北可至十七度，在南可得七度，亦 非謂諸宮交會，皆可得七度、十七度之限也。今試於 本界中論地，先論其極高四十度者；又於本地論時， 先論其不甚遠於天頂者。如日月交會在夏至鶉首 宮初度，設當時不會「於正午，其高庳差變為南北差 者必少，而所增視距度亦少，即所得者不為其最大 限。」必設實會正午月距黃道北，得其高弧七十三度 二十八分。以推高庳差一十八分○八秒，全變為太 陰南北差。依法加於二徑，折半，得五十○分五十八 秒，為黃白兩道之視距度。則所值交周度得一十○ 度，為順天府北極同高地黃道本度，月距北日食之 最大限，可食也。設月距南，則二徑折半，共三十二分 五十○秒，反減太陰南北差一十八分○八秒，得兩 道視距一十四分四十二秒，所值交周止二度五十 ○分，為本地本度，月距南日食之大限，可食也。次論 其甚遠於天頂者，設日月在冬至星紀宮初度，會亦 正午，其高弧二十六度三十○分，推得高庳差，即南 北差五十六分二十四秒。加二徑折半，得黃白兩道 總距一度二十九分一十四秒，為月實距南所推最 大日可食之限，一十七度二十四分。所以然者，人目 所見日月，以兩心合會，必在太陰所離視道交黃道。

圖

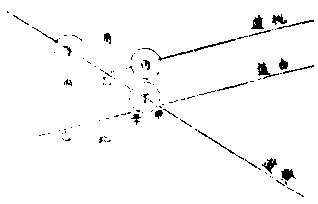
之處距其兩道實交尚一十一度又本南北差減二徑折半得距度二十三分三十四秒相當者得四度三十二分為太陰尚不及實交未過黃道南而以視差故人目所見則已過交出日食限之外矣如圖丙為太陰丁為太陽甲為黃

圖

白兩道之實交論實距度則日月至甲宜相掩而食今冬至南北差甚大太陰之視行循丙乙視道尚在己距甲遠即己切太陽周入日食之限後太陽丁行黃道至乙與太陰視道相遇是為視交即二曜以兩心合會能全食若更前至

辛，日月亦未及實。交甲，太陰實未過黃道。南而視行， 則已過太陽之南，即丙不能掩日，亦不能切日不食 矣。可見太陰實距北，在己為順天府同緯地，最大，食 限得一十七度有奇，至辛遂出食限之外。況過甲而 後實距南，其視度距太陽甚遠，安得尚有食乎？再於 木界中論地，論其極高一十八度者，先設日月在冬 至星紀宮初度，實會在正午，得高弧四十八度三十 ○分。《高庳差》全變為南北差，四十一分五十八秒，加 二徑折半，總得兩道相距一度一十四分四十八秒外此無日食在其內可食相值之食限，一十四度三 十二分，其食甚亦未至實交也。若行至實交，則太陰 以視度過交而南，四十一分五十八秒矣。以較二徑 折半，則視距為大，不已出兩食限之外乎？安得有食？ 設日月會於夏至鶉首宮初度，此在天頂北五度三 十○分，得高弧八十四度三十○分。推南北差，得六 分○八秒，以加二徑折半，得三十八分五十八秒，為 《太陰入陽曆》兩道相距度。二曜至此，即以周相切，推 得日食限七度三十一分。若月「距北，則兩半徑」減南。

圖

北差餘二十六分五十二秒僅得五度一十○分為日食限也如圖地居夏至之南目視丙月則偏北故太陰之實度在黃道南為本道上之乙與太陽之實度丁甚相遠卻以南北視差移而就近及以甲乙為食限二曜相掩必未至甲

也。若其過實，交甲至己，在黃道北，則因南北差見月 更在北，與太陽相距更遠，不復能相掩矣。

太陽、太陰越六月皆能再食。

越六月者，如寅月食申月得再食也。如左圖，甲丙乙 丁為太陰離道，交黃道於甲於乙，甲丙乙為其距北 半圈，餘乙丁甲為距南半圈，己庚戊辛皆為食限。依 《多祿》某隨迤北諸方所定中會時，甲己及乙戊入《陰 曆》，為日食限二十○度四十一分。〈地愈向北食限愈大故也〉甲庚 及乙辛入《陽曆》，得一十一度二十二分，則限外弧己。

圖

丙戊得一百三十九度庚丁辛得一百五十七度一十六分越六月之中積交周一百八十四度有奇〈先去全周〉則大於己丙戊及庚丁辛兩弧，故初月在食限內，與正交相近者，六月後則近中交，亦在食限內，而日能再食。若月食，不論《陰陽

曆》，其限皆一十五度一十二分，則己丙戊弧、庚丁辛 弧皆一百四十九度三十六分，皆小於中積交周度。 故初月交周度入己甲庚食限內，後六月又在戊乙 辛食限內，而月能再食。

太陰越五月，能再食，越七月不再食。

以距月之中積交周度，與初月食限外之弧相比，若 度贏者，則此食限內能起，彼食限內能止，即兩皆有 食。若度縮者，則一起一止，或在兩食限之外，不再食 矣。如五平月，交周得一百五十三度二十一分。〈去全周己〉 月食於高庳中處，其實限一十一度三十○分南北 同。得限外無食之弧，一百五十七度亦南北同，是皆 大於交周。弧則五平月中，不可得兩食矣。亦有可兩 食者，則大月也。太陽躔赤道南，在其最庳，左右，必速。 行同時。太陰去全周在其最高，遲行必得定朔策少 月大，交周弧亦大。夫五月之平朔，策去太陰全周得 一百四十五度三十二分中分之左右并得太陽均 度四度三十八分。又太陰五月自行一百二十九度 ○五分中分之，以最大加減，得其并均度八度四十。

圖

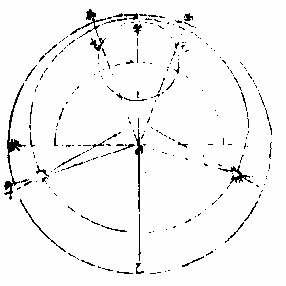
○分太陽均度應加

實度距最庳左右比平度遠故

太陰均度應減

設月逐日實未追及故

得日月以實行相距總弧一十三度一十八分為月逐日未及之弧如圖太陽從秋向春行本天小半周

「以當黃道正半周，必速行。」以甲乙直線中分其平行， 左右各得丙丁均度。太陰在本輪，自戊過最高辛至 己遲行，以甲辛平分其遲行弧左右得壬辛及庚辛 均度。日月兩均度不同類，一加一減，并之得一十三 度一十八分為太陽。以實行在前太陰以實行在後 之弧，而太陰逐太陽行一十三度，此時間太陽更行 一度○六分，以并於太陽均度，總得五度四十四分， 為五大月。過五平月之度，亦為實交周。過平交周之 度，以加平交周一百五十三度二十一分，得一百五。

圖

十九度○五分較食限外之弧贏二度○五分則月食於甲乙限內為壬距乙甚近而限外交周度壬庚越五月復可食於庚然食之分數少矣又證太陰越七月不能復食者則小月也月大或平即交周弧大於食限外之弧不可得食

圖

今太陽在其最高左右遲行太陰在其本輪最庳左右速行因而成小月夫七月之平朔策得二百○三度四十五分同時太陰自行一百八十○度四十三分如圖甲乙分日月平行甲辛分太陰自行太陽左右各得最大均度丙丁并

為四度四十二分，應減。

實度距最高，左右比平度近故。

太陰均度，壬辛及庚辛并為九度五十八分，應加。〈設月 以實行過太陽故〉一加一減并兩均度，得一十四度四十○ 分，為太陰過太陽之弧。此時間太陽亦行一度一十 分，以加其均度，得五度五十五分，是為七小月間實 行。不及其平行之度，又為七月間交周平行之弧所 減，以成七小月實行之度。今以平行二百一十四度 四十二分，去減五度五十五分，得二百○八度四十。

圖

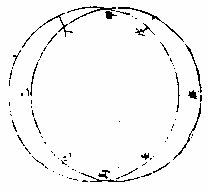
七分以加於食限外之弧

此第論太陰在其高庳中處甲丙左右四食限

為戊乙壬或己庚丁僅得二百○三度小於七小月之實交周二百○八度有奇則月初食在戊丁限內後七月不能於己壬限內再食也

圖

太陽越五月或七月皆能再食

此越五月能再食者必大月也其間交周實行可得一百五十九度○五分設日月在高庳中處得二徑折半三十二分二十○秒設太陰距度亦正得三十二分二十○秒則以前法

求得距交六度一十二分，當在乙或在丁，而乙丙丁 弧乃得一百六十七度三十六分。若太陰絕無視差 者，即食限外之弧乙丙丁大於實交周弧八度三十 一分。日月合會，先在甲乙弧內有食，越五大月復會， 必不能及丁戊為再食矣。然太陰既有南北視差，則 以交周度不及食限內之弧八度三十一分平分之 兩，加於食限，得甲己及戊辛各一十○度二十八分。 而太陰在己或在辛，皆距黃道五十四分三十○秒。 減二徑折半，餘視差二十二分三十○秒。倍之，得己 及辛，兩視差共四十五分。則諸方能得南北差及此 分者，所見太陰必偏南下掩太陽，得有食也。今所論 五大月，太陽速行，先於太陰一十三度一十八分。又 於太陰逐及時間，行一度○六分，總得一十四度二 十四分。太陰行盡此度乃及日，須一日○九刻，是為 五大月。過五平月時刻，則五大月得一百四十八日 一十八小時。故先定朔在酉正，後必在午正。若先在 午，則後在卯。又太陽五大月行一百五十一度，以最 庳平分左右，得先定朔在壽星宮二十一度；次定朔。

圖

在娵訾宮二十一度諸方地面得極高二十餘度見太陰離是二壤值是二時南北視差并得四十五分則越五月得再食此外極出地愈高南北差愈大食限愈寬凡交周在黃道北入甲己食限越五大月必入辛戊食限人居赤道北

圖

者可見兩食或交周在黃道南入戊壬食限越五大月必入庚甲食限人居赤道南者可見兩食

謂太陽越七月而再食則小月也否則交周度大於正交及中交之總食限而先在內後必在外不食矣若七小月間交周行依前

得二百○八度四十七分。而設無南北差者，則以日 月兩半徑為食限，得甲乙及戊丁各六度一十二分。 而總乙己丁弧一百九十二度二十四分，小於交周 一十六度二十三分。即太陽先食於丁戊限內，越七 月後，必己出甲乙限外，亦不食也。既常有南北視差， 則以較餘交周弧一十六度二十三分平分之，以加 於甲乙及戊丁，得甲壬及戊癸二限，各一十四度二 十三分，而壬己癸與交周弧相等。又甲壬及戊癸一 十四度二十三分，得相值之距度，一度一十三分三十八秒。減二徑折半，得四十一分一十八秒，為各視 差。倍之，得一度二十三分，則諸方有此視差者，得有 食也。今所論七小月，太陽遲行後於太陰，共一十四 度四十○分，為太陰一日五小時所行之弧。是一日 五小時者七小月，不及七平月之時刻也。總七小月， 得二百○五日一十二小時，故越七月得再會，先會 在卯，後會必在酉。又太陽行七小月，實得一百九十 八度。〈前已證〉從最高平分之，得先會太陰在娵訾宮二 十七度，後會在壽星宮一十五度，則凡離是二壤，值 是二時，所見太陰南北視差并得一度二十三分者， 必越七月得再見日食也。此為極出地三十四度以 上。蓋距赤道愈遠，視差愈大，所見食分愈多矣。

《食分》第二。〈凡四章。〉

欲知此月內有無交食，則以《食限》求之。〈見上文〉「欲知此 食，食分幾何，則以距度求之。」距度者，在月食為太陰 心實，距地景之心，兩心愈相近，月食分愈多，在日食 為日月兩心。以視度相距，其近其遠，皆以目視為準， 不依實推。蓋定朔為實，交會天下所同，而人見日食， 東西南北各異，所以然者，皆視度所為也。日食詳說 見後篇。此先解月食分，則論定朢實會人所見者，東 西九服各異，南北《天下不殊》也。如左：

太陰食甚分數

太陰在食限內過地景，其兩心最相近時為食甚，而 食分必多。欲知食甚之處，用距度求之，蓋距度與地 半景及月半徑相減，得月入景之分。

此言「分」 者，天周度數之分，非平分月徑之分也。稱分有二類，見下二文。

如兩半徑得一度，距度四十○分相減，餘二十分，為 所求月入景之分也。但距度與半景或等或不等，若 過不及之分小於月半徑，則月不全入景，而止食其 半或太半或少半而已。若距度小於半景者，為太陰 之正半徑，則雖全食，隨復生光，其食分即太陰之全 徑。以月自行推之，若絕無距度，即太陰遇景正在兩 交，則并其兩半徑，可推月食之分也。

假如甲乙為地景。

《定》朢時月入此則失光，亦名「闇虛。」

圖

之半徑乙丙為太陰半徑總得甲丙為月食限限者乙點為二周相切之處食從乙點起漸入漸大若兩周相分於乙點則不食也食有三等一曰不全食二曰全食三曰正食不全食者如一圖甲丁為黃道丁辛當白道月心在辛即入

圖

景者半是為半食或月心在庚則如二圖入景者大半是為大半食或在戊則入景者少半為少半食皆不全食也求食分法以距度減二徑折半如圖甲己與甲丙等為二徑折半甲戊為距度以甲戊減甲己餘戊己戊己與辛庚恆相

圖

等故於二半徑減距度即得其入景辛庚為此食之分也全食者如三圖月心在戊距度甲戊兩道如前而距度入於半景者為太陰之半徑戊己則己庚入景之分為全徑但全入以後太陰或向交行欲至丁或離交行欲至辛其周旋出景外則無既內分矣

圖

以上二者皆有距度則皆不食於交點皆偏食也若第四圖太陰食甚時絕無距度則月心與景心皆會於甲甲乙為半景徑甲戊為半月徑兩半徑并為甲丙設甲乙丙為黃道甲丁為白道太陰從丁行以戊

邊至甲己，全入於丁甲半景之內矣。又行至邊及戊， 乃食甚，故更得甲、戊為既內分，總得丁、戊兩半，徑并 為此食之分。此月食之最大，食於交點者也，正食也。

食分二類

求食分之大幾何，有二類：其一為天周度數之分，如 上文所論者皆是也。月食之最大者，可得一度○四 分有奇。其一為太陰本徑之分，則惟曆家所命。如命 月體之全徑為十二平分，則最大食得二十二分五 十四秒也；如命為十平分，則最大食得一十九分○五秒也。又此二類者，皆係太陰及地景之視徑，雖距 度同分，而大小多寡，猶多變易。設距度恆為二十五 分，因太陰自行在最高，得月食度數之分為三十三 分一十五秒；太陰在最庳，得食度數分為三十九分 二十○秒。其自行在一宮或在一十一宮。〈俱近最高〉得三 十三分三十八秒。在二或十宮，得三十四分三十六 秒。在三或九宮，得三十六分。在四或八宮，得三十七 分三十○秒，在五或七宮。〈俱近最庳〉得三十八分四十五 秒。如前法，以太陰半徑半景并，每去減二十五分，即 得此食分之數。他距度依此推之，其所繇漸漸有差 者，則因太陰距其最高，愈遠即視徑愈大故也。又平 分本徑亦有多寡，有大小。蓋太陰在最庳，其全體之 天度分為三十四分四十○秒，得平徑一十○分。設 食甚正在交點，無距度，則二徑折半，得天度一度○ 四分二十○秒。推總食之平徑分，得一十八分三十 四秒而一，平徑分當天度三分二十八秒。又設太陰 在高庳之中，食甚距度如前，其平徑亦一十○分。以 兩半徑推總食，得一十八分四十四秒而一，平徑分 當天度三分一十五秒。與前不同，則以視徑，故更設 太陰在最高，其視徑更小，僅得天度三十○分三十 ○秒。食甚在交皆如前，亦得平徑一十○分。而所推 總食分更多於前，為一十九分○五秒，則一平徑分 當天度三分○三秒。可見距度同、平分徑同而食分 不同者，月自行有高庳，其去地之遠近異，視徑亦異 故也。

求月食徑分

「太陰入景」，以本徑分明暗之限，為人目所見之分。若

圖

全食更加入景之餘分〈即既內分〉推得總食分，則距度能翕張其二徑，為食分多寡之緣也。今或依第三卷所定《太陰及地景視徑表》，用引數求之，并而去減其距度，則太陰視徑與十平分。若其二半徑減距度之餘分與食分，或依第二卷前。

圖

所設求太陰均度之圖用甲乙丁三角形求之蓋乙甲丁太陰均度角之正弦與乙丁直線若甲乙丁總自行餘弧角之正弦與甲丁直線既得甲丁為太陰距地遠次求太陰視徑則其距地遠甲丙與太陰實徑之正弦丁乙若全數與

丁丙乙角之切線，次以太陰半徑與地半景大小之 比例，為一五○與四○三。推地景視半徑。蓋一五○ 與四○三，若太陰視半徑之正弦，與景視半徑之正 弦也。既得視半徑，用三率法，如前推算食分。欲用表， 則於引數查視半徑，而以月視徑及兩半徑減距度 之餘數查食分。然表中列數，從引數出，其理一也。

求月食面積分

前論「月食分」，皆目可見、器可測之視徑分也，若求其 不全食之面，入景之分，則有別法。設甲為地景之心。

圖

乙為太陰之心以距度得其兩心相距為甲乙直線又先得甲丙為地景視半徑得乙丙為太陰視半徑則甲乙丙三角形內有其三直線可求三角又甲乙丁三角形與甲乙丙三角形等則以丙甲丁總角得丙戊丁弧亦以丙乙丁總

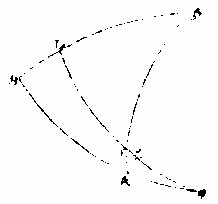
圖

角得丙己丁弧今欲以徑與圈之比例推丙戊丁及丙己丁兩弧與其本圈半徑同類之分若干

弧曲線與直線異類以周徑法變曲線分為直線分故曰同類

其法以甲丙及丙戊得景中丙甲丁兩半徑弧形

兩半徑弧形者，兩半徑為兩，腰弧為底，求得其容積也，說見《測量全義》第三卷。

亦以乙丁及丁己得月上丙乙丁兩半徑弧形。又丙 丁直線為等腰兩三角形之公底線。求其半，得丙辛； 以乘甲辛，得甲丙丁三角形之積；以乘乙辛，得乙丙 丁三角形之積。次以兩三角形之積，各減其兩半徑 弧形之積，所餘丙戊丁己長圓形，為太陰入景之面， 可得其餘不入景之面也。

假如崇禎五年壬申九月十四日夜朢，月食四分四

圖

十二秒食甚太陰距度四十四分其視半徑一十六分二十五秒地半景四十三分二十三秒設甲乙為距度乙丙為月半徑甲丙為景半徑則最大線甲乙與餘兩腰線甲丙丙乙若兩腰線相減之餘線甲丁與大線之分也即算得大

圖

線之分甲戊以其餘平分之為戊辛辛乙次從丙作丙辛必為甲乙之垂線矣既得各線如圖皆通為秒以求甲角及乙角則甲辛與全數十萬若甲丙與丙甲辛角之割線算得甲角二十一度四十○分倍之得四十三度二十○分為

丙戊丁地景之弧。又辛乙與全數，若乙丙與辛乙丙 角之割線，算，得乙角七十七度○六分，倍之得一百 五十四度一十二分，為丁己丙太陰周之弧。次求其 各與本圈半徑同類之分，則月徑及地景徑各與其 本周若七分與二十二分也。推得地景周一六三六 一，月周六一九一。因此用丙戊丁及丙己丁兩弧，各 求其本圈徑同類之分，則全周一六三六一，與所截 丙戊丁弧之分。若全周三百六十度，與本截弧四十 三度二十○分算得一九六九，為丙戊丁弧，其半九。

圖

八四為丙戊半弧也又太陰全周之分六一九一與丙己丁弧之分亦若三百六十度與本截弧一百五十四度一十二分算得二六五一為丁己丙弧半之得一三二五為丙己半弧也次以甲戊乘丙戊得丙甲丁地景兩半徑弧形之

圖

積二五六一三五二以乙己乘丙巳得丙乙丁太陰兩半徑弧形之積又丙甲辛角之切線〈乙丙也〉與丙辛若全數，〈甲丙也〉與甲辛，得丙辛九六○，則彼此求兩等邊起線三角形之積與求兩半徑弧形之積，通為一法，得甲丙丁三角形之積

二三二二二四○，乙丙丁三角形之積二一一二○ ○，各減其兩半徑弧形之積，得丙辛丁戊分圈形之 積二三九一一二，丙己丁辛一○九三九二五，并之 得總數一三三三○三七，即丙己丁戊全形之積也。 又以太陰半徑九八五，乘其半周，三○九得三○四 八五七五，與總數比，得太陰入景之面與其未食之 面，若一十三分與三十○分也。

食甚前後時刻第三。〈凡三章。〉

食甚前，初虧也；食甚後，復圓也。兩限間之時刻多寡， 其緣有三：一在太陰本時距度，因距度或多或寡，每 食不同，即太陰入景淺深不同，淺則時刻必少，深則 時刻必多。其二，在月及景兩視，半徑，半徑小，太陰過 之，所須時刻少；半徑大，太陰過之，所須時刻多。其三 在太陰自行，自行有時速，有時遲。雖則距度同、視徑 同，而自行遲疾不同，即所須時刻不同矣。推距度及 視徑，皆依前所設法，此專求太陰實行，以定食時刻 分。

月食起復行度

圖

太陰入景自初虧至食甚之弧與其出景自食甚至復圓之弧兩者略相等故求其一倍之得在景之總弧如圖甲為景心躔甲乙黃道乙丙為白道太陰心至丁為初虧在丙為食甚復圓在戊丁戊者天周之弧也而所截弧極小故作

圖

直線用之又甲乙丙三角形也而乙角極小乙丙與乙甲略等故作平行線用之因而甲丙可為垂線因而丁丙與丙戊亦可為等今自甲出兩直線為甲丁為甲戊皆當太陰地景之兩半徑而甲丙為太陰距度故甲丁戌三角形以甲

丁方，減甲丙方，得甲丁方，其根為太陰初虧至食甚

行過太陽之弧。若不用開方，則有別法。以角求對邊 線，如甲丁線與丙直角，若甲丙線與甲丁丙角，既得 丁角，餘為丁甲丙角，則丙直角與甲丁線，若甲角與 月行景之半線丙丁也。雖食分不同，或半月入景，或 全體在景。求初虧至食甚之弧，恒倣此。次求食既至 食甚亦倣此。倍之，得太陰全入景至生光及復圓之 總弧。如左圖甲乙為黃道，乙丙為白道。太陰心行至 丁則全入景，既至戊即生光，得丙丁及丙戊略相等。

圖

故先得丙丁倍之即丁戊也此則以甲丙為距度甲丁為地半景減月半徑之餘於甲丙丁三角形用此兩線及甲丙丁直角推丙丁線與前同法若欲精求之不聽甲乙乙丙為平行仍作兩線斜交於乙太陰初虧在丁食甚在丙復圓

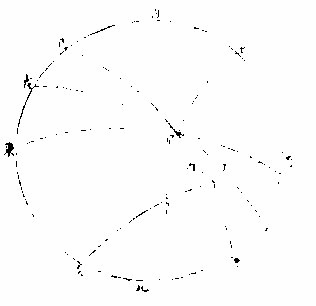
圖

在戊丙丁是太陰在景之半為距交一十二分之一即作丁庚線與甲乙平行取丙庚亦丙甲距度一十二分之一以減甲丙得甲庚是太陰初虧之距度以加甲丙得甲己是太陰復圓之距度次以甲丁甲庚兩線及庚直角求得庚丁

線以庚丁庚丙兩線及庚直角，求得丙丁線，為初虧 至食甚行度。後以甲己、甲戊兩線及己直角，求得戊 己線，以戊己己丙兩線及己直角，求得丙戊線，為食 甚至復圓行度也。

食甚距度線與白道，當為「垂線。」

求食時刻設太陰食甚前行度與食甚後行度等，即 距度線必當為白道之垂線，不然者，必行度前後不 等，而時刻亦不等。如左圖甲乙為白道，甲丙為黃道， 太陰在丁，自庚黃極出線，過丁月為庚丁弧至戊黃。

圖

道指太陰實度在戊因太陰在丁得交常分甲丁而庚丁與庚乙若甲丁與甲戊〈皆用正弦算〉若得甲丁四十五度，與甲戊最差之限，得六分。

甲戊少於甲丁在圖為己丁

若甲丁在食限內其與甲

戊，差又不及三分矣，因兩道之最大距不過五度故 也。設甲丁弧得二十○度，而以甲乙與乙丙之比例， 推甲丁與丁戊，得丁戊距度一度四十二分。今作戊 己與甲乙為垂線，又以甲丙與丙乙之比例，推甲戊 與戊己，亦得戊己相距一度四十二分。可見丁與己 見有差，戊己與戊丁有微差，不足見也。今不用戊丁 開方，而用戊己，又以戊己平分太陰入景與出景之 弧，其不得有差甚明矣。

太陰食在景時刻

前第二卷論月食以食甚時為主，於食甚前之初虧， 至食甚後之復圓，總推定時刻分秒。其法以太陰在 景中行度變為時刻，如先得食甚前行度，求所當初 虧至食甚時刻，倍之得其餘行度，亦變時刻。皆依先 所定行度，用比例法推筭也。如崇禎五年壬申三月 朢，太陰初虧至食甚，行四十○分一十六秒，欲變時， 用三率法。太陰行三十三分一十一秒，得一小時。今 四十○分一十六秒，應得一時一十二分四十三秒。 但太陰自行恒異平行，食時間恆不居本輪之一處， 故所用一小時之行分，以定食間行之時，不得用平 行，必須考將食之實行。查太陰實行時表法恒以自 行宮度得一小時之實行，每度所值，各各不同。如太 陰平行一時，得三十○分二十九秒。以本時自行求 均度，或加或減於平行，得實行。若加減度表對自行 初宮三十二分四十○秒，得均度二分四十六秒；以 減三十○分二十九秒，得二十七分四十三秒，為表 中相當引數初宮初度之率也。加減度表對自行一 宮三十二分四十○秒，得均度二分二十五秒。以減 一小時之平行，餘二十八分○四秒為相當引數一 宮及一十一宮之率也。其餘皆倣此。第自行在本輪 最高左右，必減均度，得一時之實行；在最庳左右，必 加均度，得一時之實行耳。

既以實行推定總時刻，則以食既至食甚之時，減先 定食甚時刻分秒，得食既時刻分秒。以相加，得生光 時刻分秒。又以減食甚前總時，得初虧。以相加，得復 圓。又以初虧減復圓，得總食之時刻分秒。若初虧在 子時前，復圓在子時後，則即以丑初為十三時{{Annotation|，午正起算 〈用小時〉丑正為十四時，如是接續減之。

《交食圖義》第四。〈凡三章。〉

求日月失光之面向何方位，則有兩緣，其一從太陰 距黃道度作大圈，令過太陰、太陽兩心。〈此日食也〉或「太陰」 與「地景」兩心。〈此月食也〉下至地平，周遭移指交食所向之 方也。其二黃道斜交於地平，日月隨之行，遇食必有 時向東南、西北，有時向東北、西南也。欲繪《交食圖》，必 先察日月所向，起復方位。第舊法祗以陰陽二曆分 別南北，殊粗率。今法必可得其度分，頗為繁細耳。

圖

距度變日月食所向方位

太陰食起復之間以本行屢遷其度分即作過兩心〈月心地景心也〉「大圈至地平時刻各異，所向方位亦時刻各異。欲盡推之，其多無數，故當求其初虧。」食既、食甚，生光復圓，五向而止，如《圖甲》。

圖

為地景心甲乙為黃道戊丙為白道兩道之大距不遠故作平行線論初虧太陰在丙食既在丁食甚在戊即甲丙甲丁甲戊皆過月地景兩心之弧因太陰漸近於地景心甲其距度遠近漸次不同而乙甲丙角乙甲丁角乙甲戊角之

小大亦不同，則太陰所向地平之方位度分亦不同， 故恆以本距度推本角。如甲丙初虧之距，為半景月 半徑，并之甲丁食既之距，為半景減半月徑之甲戊 食甚，則為太陰之正距度也。甲戊丁角可當直角，不 論其甲戊線與甲丙戊對角，若甲丙線與丁戊甲直 角，得甲丙戊角與乙甲丙角相等。〈乙甲丙為所求〉又「甲丁戊 三角形」，依此法推甲丁戊角與乙甲丁角。〈此為所求〉「相等 而食甚乙」，甲戊為直角，故在甲。諸角「其線不等，即所 向方位不等。」論日食，則甲丙為日月兩半徑，甲戊為

圖

太陰距太陽食甚之視度以求甲丙戊角向下皆同前法今更作圖甲為景心乙丙為黃道若太陰初虧在乙其入景之面必正向東若復圓在丙

初虧在乙復圓必不在丙故曰若指他食也

其出景之面必正向西皆

無距度，故若其距北在丁或在戊，即入景之面向東 南或西南；若其距南或在己或在庚，即入景之面向 東北或西北也。論日食，設甲為太陽心，其理同此，但 出入之面所向，與月食所向正相反，此為異耳。

《黃道出沒變》日月食所向方位：

黃赤兩道之兩交切地平。若一在正卯，一在正酉，不 偏南北，即諸方俱無闊度矣。外此或黃道距南，或距 北，其距漸多，其出沒之闊度，去離卯酉亦漸多。又南 北極愈高，其相離更遠。如北極出地三十六度，黃道 度去離春秋分或南或北一宮，其闊度左右各一十 四度一十五分。若去離二宮則更遠，其闊度各二十 五度一十三分，最遠者得二十九度二十九分。若北 極出地四十度，即一宮得闊度一十五度○四分，二 宮得二十六度四十五分，最遠則三十一度一十九 分也。太陰既隨黃道行，其食也亦必依其闊度，則起 復之所向方位，太陰亦必依闊度之左右也。今欲定 其多寡如左圖：南西北東為地平圈，丁甲戊為黃道 食時，得闊度。戊距正東若干，太陰心在丙，景心在甲。

圖

過兩心之庚甲己大圈指己因戊黃道度距正東遠己隨之距正東亦遠而丙月之初入景所向為己也今求東己弧先設辛為天頂出高庳弧過甲至壬為頂極圈又作一癸午弧與甲庚為直角次甲乙丙小三角刑有乙丙距度有甲

丙兩半徑有甲乙丙直角，依比例推得甲角。次以食 時及甲景所躔黃道度，得戊甲辛角，即得。其餘辛甲 乙角。又得辛甲乙所分之辛甲午角。〈減乙甲丙小角〉次甲辛 午三角形，有甲角，有午直角。又以北極高及黃道距 赤度，得甲辛弧。可推得辛午線。以加辛癸象限，得午 癸總弧，為午己癸角，其餘角為甲己壬也。而己甲壬 為辛甲午之對角，甲壬為辛甲之餘弧，因可推壬己 弧。又戊甲壬三角形有原，推之甲戊，有甲壬戊直角， 有乙甲辛相對之壬甲戊角，因可推壬戊弧。去減先得之壬己餘，己戊為所求太陰初入景所向東南維 之地平經度；以加初所得東戊弧，則得東己總弧。

月食圖

《西曆》恒推日月食所向方位，以其所虧及復圓距度 作圖，求距度食甚前與食甚後。為一法，以太陰自初 虧至食甚之實行，加入太陽同時所行分秒，得太陰 初虧至食甚在景之總分。以加前所定食甚交常度， 得復圓交常度；以減，得初虧交常度。次求初虧距度， 則全數與其交常度若黃白之大距度與其距度。求 復圓距度倣此。

假如崇禎五年壬申三月朢，太陰初虧至食甚景中 行過太陽四十○分一十六秒，為時四刻一十二分 四十三秒，同時太陽行二分五十七秒；以加前行，得 四十三分一十三秒，為太陰在景之總行。其食甚交 常度，為過中交八度三十五分五十八秒；以加太陰 總行四十三分一十三秒，得復圓交常度一十○度 一十九分一十一秒。其正弦一七九一四。以減。得初 虧交常度，七度五十二分四十五秒。其正弦一三七。

圖

一○算得太陰初虧距度四十一分復圓四十九分三十○秒若用表以時分查太陽本行以交常度查太陰距度更易得矣欲依本食作圖其外大圈之半徑為月半徑地半景并得一度○四分三十二秒

圖

量用比例規或先平分一直線

內取食時所得地半景

此為四十六分三十五

秒

作內圈以當景次查距度此食在南初虧四十一分復圓四十九分得太陰初在乙後在丁食甚亦依其

距度在丙，為食之定分。圖上下左右書四方，其起復 所向方位，必與天合也。〈以上原本曆指卷十二交食之四〉

《視差》以人目為主第一。〈凡四章。〉

前言「實會」、「中會」、視時、食限等，皆日月食之公法也，是 皆準於地心。今再論月食生於地景，景生於日，故天 上之實食，即人所見之視食，無二食也。日食不然，有 天上之實食，有人所見之視食，其食分之有無多寡， 加時之早晚先後，各各不同，推步日食，難於太陰者 以此。其推算視食，則依人目與地面為準。

視會

「凡交會者必參相直，不參直不相掩也。」日之有實食 也，地心與月與日參，居一線之上也。其有視食也，人 目與月與日參，居一線之上也。人目居地面之上，與 地心相距之差，為大地之半徑。則所見日食與實食 恆偏左偏右，分為兩直線，各至於宗動天，其所指不 得同度分，是生視差。而人目所參對之線，不得為實 會，而特為「視會。」

如左圖，甲為地心，乙為地面，丙為天頂，若丁為日戊。

圖

為月即在甲丙一直線上則實會即為視會因地心與人目無分線故也若日在辛必月至壬方與地面乙作一線為視會矣若月至己與地心甲作一線則實會也今言交食惟以目見為憑故日食全論視會若所居地面不同即食分

圖

多寡加時早晏亦隨之異也又視會實會在日月本天皆無度分可指而全依宗動天之黃道圈度分則此實會線所指謂之實度視會線所指謂之視度如圖甲辛線所指為黃道之庚則庚為太陽之實度若乙目視辛日至黃道癸視

「己月至黃道午」，則癸為太陽之視度，午為太陰之視 度也。

《日月目見之度，非實度》。

譬之畫圖者，作平圓形，則一舉手一運規即得矣。若 欲為螺旋線，先須依法作識，又依法作線，乃成形焉。 測天之法，亦猶是耳。今欲知日月躔離，東西南北，亦 轉儀闚表，一覽可知。若欲定其本行所在，則非聊一 寓目，遽能得之，必先後累測度分，展轉較勘，乃可定 也。假令目居地之中心，〈地之心即宗動天之心〉「極目所見，則有恆星，以當彼界，兩界中間，有日月五星，是名七曜。七 曜相視，有遠有近，無有同者。」即論一曜，亦各時遠時 近，無時同者，是則目所能見也。然因目所見，得其視 度於彼界，因以視度測其與某恆星相距若干度分， 因以是度推其實與地相距若干遠近，則可，謂即目 所見，遂得其實。行能分別其去地遠近則不可。何者？ 《七政》諸本天雖居恒星天之內，乃不見火、木、土等內 天之星，以本體能掩最外之恒星，則何從辨其內外 遠近乎？又目所見者，太陰太陽二體相若，何從知其 內外之相距絕遠，二體之小大絕不相等乎？內天之 兩星，參對於外天之兩經星，目見之，能知外者之兩 相距甚遠，內者之兩相距不甚遠乎？是三者皆目力 難憑之效也。或曰：「是則然矣。測量之法，皆憑目所見 也，則可廢乎？」曰：何可廢也？惟測內天之星，得彼界所 指之點，以為即在恆星之天，聊可得之矣。何者？凡用 在界之弧，以測其輳心之角，無弗真者。目測恆星之 天，其在地面與其在地心也，無以異。

《地居恆星》天中止當一點。

若測內天諸曜，目雖不在地心，相距亦不甚遠。故測 日月五星，於彼界上得點，即與實度相近。

曰：「聊可得之」 ，曰「距，不甚遠，曰近。」 其實度皆因有地半徑視差故。

但恆星有時不見，或與內天諸曜不相值，故曆家以 「地平」代恆星，更用遠視之器以助目力，得日、月五星 之視度分。依法推步，乃正得其實度分矣。

人視差

兩目。�《存》，不惟相助以為明，相代以備患，亦能彼此 互用以察物之遠近。蓋各以其心。〈目睛最中之一點為心〉受外 物之象。其過心之兩直線，至物體則相遇為兩腰，兩 睛心自相距為底，成三角形。因以其比例之大小，別 物距目之遠近，是謂「目差。」緣此可推，天上之視差，以 小喻大，其理一也。若物大遠於人目，則底線極小，兩 腰極長，是過睛心之兩徑線，與平行無異，正如地球 比恒星天之高，特以一點為底，視差無所繇生矣。 如左圖兩目之心為甲為乙。目所視之物為丙。若甲 乙線。可比於甲丙線。〈可比者不甚遠則有比例〉則兩戊己徑線漸。

圖

相就如己而相遇於丙若物更相近為丁則兩徑速相就為辛庚

甲乙丙及甲乙丁兩三角形皆等邊又同一底線則丁角大於丙角而丁甲乙角必小於丙甲乙角

而兩目之光線皆從己斂

向於庚，自覺所視之物變遠為近矣。若物與目相去 甚遠，則無比例者，因兩徑絕難相就，絕難相遇故也。 今借此理明視差之公理。如本圖設丁物之前，有橫 堵為壬癸，令甲目獨視丁物，則所見若在壬，令乙目 獨視丁，則所見反在癸，而丁前丁後兩交角，形必相 似，即丁物亦不遠於壬，不遠於癸。蓋視之目分兩線 為交角，即能分本物之遠近也。若不能分兩線，即不 能分遠近。

地半徑差

《目視星》欲辨六曜。〈月五星也〉恆星之內，勢不能也。則當 借地體之大，補目力之不及。法用地半徑為底，以推 測量所指之界，即可得七政遠近上下，各居本天之 實處。如左圖甲乙兩目相距為底則二寸耳。今以兩 地相距數千里或數里當之以為底，如甲為順天府， 乙為廣州府，丁為太陰，兩人同測之，一在甲，一在乙， 因此大底之遠近，比於各距太陰之兩腰，得大小之 比例。則甲丁及乙丁兩直線，必覺彼此相就，以趨於 丁矣。再使壬癸為列宿天之兩恆星。

圖

或壬癸為太陽之全體壬當其南周癸當其北周

測者一從甲見太陰丁若在壬以本體合於一星之體

或太陰之南周齊太陽之南周

一從乙測太陰反在癸轉

圖

就北以合於他星〈或太陽之北周〉若《甲乙》兩測之距愈相遠，即所見丁月兩指之極高亦愈相遠。

一偏南一偏北東西亦同

而人在甲能見太陰掩日為日食人在乙即不可得見矣以此壬癸當宗動天

上之《弧正》所謂「視差」，與前言目見之「小視差」，其理一

也。第兩人相距千里萬里，同時並測太陰，其勢甚難， 故立別法代之。

詳見本書第六卷，下文略言之。

假令人正居地心，推其所得太陰距天頂應若干度 分，又同時居地面者，實測太陰距天頂得若干度分。 兩度之差，即所謂「視差」也。如圖甲乙丙為地球，丁為 天頂，甲戊丁直線所至也。若太陰在此線左右為己， 從甲地心測月，見之當在庚；自地面乙測之，乃在辛。

圖

則先推定丁甲庚角或所當之丁庚弧後推丁乙辛角或所當之丁辛弧

乙距甲與乙距丁無比例甲乙至小故

以兩角或兩弧相減得視差之弧庚辛

問一星距天頂測其宗動天上所指度分在地心測

圖

之則距近在地面測之則距遠若論角則地面之乙角大於地心之甲角何以證之其故何也曰因其一遠一近如圖太陰在本天其距頂之弧為己戊己戊之距地心甲與其距地面乙遠近之差則目所能識也所能分也

圖

因地之半徑與月本天之半徑有比例故

則目之在甲與在乙所受己戊弧之象實不能無大小為己戊弧等而兩角之大小不等

目受物象皆以角形見交食第一卷

相近者必大遠者必小也

「角既有大有小，所相當之弧不得不有大小，則辛之 距天頂，視庚之距天頂不得不遠矣。」又論辛庚視差， 實為辛甲庚角所定，何用辛巳庚或甲己乙角乎？曰： 「甲乙線與甲庚線無比例。」〈小大絕遠故〉而甲乙與甲己則 有比例，即甲己與甲庚亦無比例也。既甲乙與甲己 同為微末，不以入算，則用辛巳庚角代辛甲庚角無 以異矣，若論角，則丁乙辛角與丁辛弧相當。〈因甲乙與乙丁 無大小之比例〉又丁乙巳角，與乙甲己及甲己乙兩角并等。 〈見幾何第一卷十六題〉則兩角并亦與丁辛弧相當矣。今丁庚 弧既與丁甲庚角相當，則餘弧庚辛必與餘角甲己 乙或辛巳庚相當也。