| 欽定古今圖書集成 曆象彙編 第一百六卷 |
欽定古今圖書集成曆象彙編曆法典
第一百六卷目錄
測量部彙考七
新法曆書四〈測天約說下〉
曆法典第一百六卷
測量部彙考七
编辑《新法曆書四》
编辑
測天約說下
编辑宗動篇第三
《總論》:〈凡二條:〉
論宗動有二端。一言本天之點與線。二言本天之運 動。
三曜皆有兩種運動,宜以兩物測之,猶布帛之用尺 度也。《七政》恆星,皆一日一周,自東而西,則以赤道為 其尺度。又各有遲速本行自西而東,則以黃道為其 尺度。凡動天皆宗於宗動天,故黃赤二道皆繫焉。〈三曜 者日月星也〉
論《本天之點與線》,〈凡三章。〉
《論赤道》,〈凡七條:〉
赤道於諸大圈為最尊,其義有三:不知赤道,則諸大 圈無從可解,一也;赤道之理特為易明,二也;一日一 周,乃「七政恆星之公運動,赤道主之,三也。」
其兩極,即《大圜》之兩極。何者?為本道與天元赤道相 合為一線,動靜雖異,終古不離也。
「大圈之心、中圈之心、赤道之心」、「地之心」,同是一點為 「赤道」,與大圈、中圈同為「大圈」故也。
赤道既為大圈,其分數亦有半圈,有象限,有三百六 十度及分秒,其算數則從一至三百六十,與黃道地 平異。黃道分十二宮,各以三十為限;地平分四象,各 以九十為限。故赤道亦有過極經圈。一百八十,為用 甚大。其左右旁各有距等侶圈。〈即緯圈〉每至極各九十。
圖
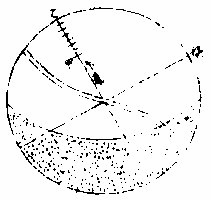
不甚為用為與天元緯度一一同線故
其用則以赤道之經緯度測各點之所在命為各點赤道經緯度
如上圖赤道上任設甲點從赤道初點乙數至甲為幾度分即甲點之赤道經度分也為在赤道上故無
圖

緯度
若所設甲點在赤道外則於過極大圈數甲點至赤道交即定赤道初點至設點之經度為六甲點至赤道即所容之緯度為五凡分南北大分獨六合之內〈即大圜也〉及日,以赤道分之,他則否。
圖

論黃道〈凡十條〉
黃道亦大圈也兩交於赤道兩交之間最遠於赤道者二十三度有奇
黃道之兩極去赤道兩極亦二十三度有奇與二道相離最遠之數同也如上圖甲至丙為黃赤二道相離最遠之二十三度
《有奇》,則庚至戊,亦黃赤二極相離之二十三度有奇 也;
黃道分數,其四象限三百六十度,與赤道同。又十二 分之為宮,二十四分之為節氣,七十二分之為候,與 赤道異。十二宮曰元枵、娵訾、降婁、大梁、實沈、鶉首、鶉 火、鶉尾、壽星、大火、析木、星紀。後曆家從便命之曰子 亥戌酉申未午巳辰卯寅丑。
節氣曰「冬至、小寒、大寒、立春、雨水、驚蟄、春分、清明、穀 雨、立夏、小滿、芒種、夏至、小暑、大暑、立秋、處暑、白露、秋 分、寒露、霜降、立冬、小雪、大雪,每一節分為三候,節氣 中以二至二分為主。」
黃赤道交處為春、秋分,相離最遠為冬、夏至。
黃道,左右各八度,以定月五星出入之道,名為《月五 星道》。〈又名六曜道下文通用〉諸曜出入於黃道度,多寡不同,最 遠者八度也,又總名為「黃道帶。」〈古法左右各六度〉 如左圖平分二十四氣者,為「黃道帶。」甲至乙廣八度, 丁戊己庚為赤道圈,辛壬癸為夏至圈,子丑寅為冬 至圈,丙則地心也
圖

周天分十二宮非獨宗動天之面也凡六合之內〈即大圜〉一切所有,從宗動之面下至地心,皆以十二分之。故凡言宮者有四義:其一,黃道帶上有一長方面,為甲、乙、丙、丁,甲乙長三十度,乙、丙廣十六度,凡七政、彗孛等從地心作直線過本點至此面之某度分即命。
圖

為本點在本宮之某度分其二以甲乙丙丁為面從地心戊出四線上至方面之甲乙丙丁各角成銳角體凡六合之內一切所有但入此銳體中即命為在本宮之某度分其三為宗動天之內規面十二分之
圖
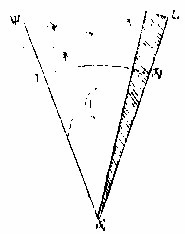
一以黃道兩大經圈各至極之己庚為首尾中相去三十度之辛壬為腰其中容即此分面也則凡諸點之在其面或在其下者皆命為在本宮之某度分其四己辛庚壬為面從面分至地心癸為橘房體則入此體中者皆命為本宮之
某度分。
黃道有經度。〈一名長度〉有「緯度。」〈一名廣度〉從黃道作過極圈,以 定其經度,法與赤道同,但本道本極異耳。若起算,從 春分始,其義有二:一為是黃赤道二大圈之交也;二 為其為大圜之中。中者,二極之間也。
黃道之過極圈,容其各緯度限各經度;其左右侶圈, 限其各緯度容各經度。
《黃道比論》。〈凡八條:〉
《比論》者,一與赤道比,一與地平圈比,一與地平南北。
圖

圈比
與赤道比論
黃赤道之交為春秋分從此作過極大圈名為極分交圈從二道最遠處作過極大圈為極至交圈此二大圈分黃赤道各為四分每分各為九十度
如上圖甲乙為赤道極丙
丁為赤道,戊己為黃道,庚為二道之交,則甲庚乙為 極分交圈,甲丙己丁為極至交圈。
黃、赤道相距,不用黃道之緯度。〈經緯線交為直角一名廣度〉而用 赤道之緯度。
從黃道出線與黃道為斜角,至赤道作直角,名「偏度。」
如降婁宮三十度,若用廣度,則相距十三度,今用偏 度,則十二度半。所以然者,為黃道斜迤。若用廣度,則 分及一象限,無法可分矣,不若用赤道之平直四象。
圖
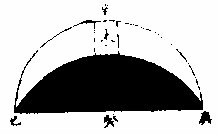
皆通也
本以黃道之三十度立算而用赤道之侶圈且與赤道為直角與黃道為斜角故名為赤道上之黃道偏度非從赤道目為偏度也其在赤道自名旁度侶度
黃道一象限九十度各有
其偏度最遠者,二十三度有奇,不言三百六十者,「餘 三象限與一同理」故也。
如右圖甲丙為黃道弧,若廣度則值甲乙,偏度則值 甲丁,即作庚丙丁辛去離圈,丙丁在其上為距度。 測黃道弧之經度,亦不用黃道之經度,而用赤道之 經度。如降婁宮本三十度,以赤道測之,則二十七度。 為此宮之黃道斜而長,赤道直而狹,故不命降婁一 次。黃道上之長度曰「三十」,而命赤道上之黃道升度 曰「二十七也
圖
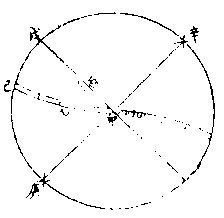
本以黃道三十度立算而用赤道經度二十七其去離圈與赤道為直角名為赤道上之黃道升度非從赤道目為升度也在赤道自名上度
如上圖甲乙為黃道弧若長度則值甲丁升度則值甲丙於赤道上命甲丙曰黃道之升度
圖
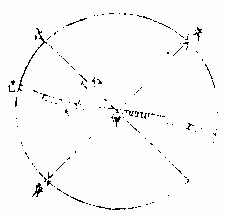
從黃赤交至北最遠黃道圈上有九十度每度作一圈與赤道距等圈平行其初圈則赤道也其第九十為夏至圈南迄冬至亦然是名日轍圈亦曰日距圈如上圖甲乙為赤道丙丁為黃道辛丁為冬至圈丙
圖
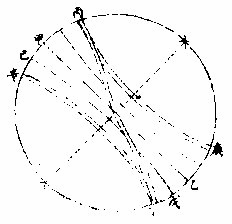
庚為夏至圈己戊等皆其日距圈也
赤道緯圈去極二十三度有奇者過黃道極名為極圈南北同
如上圖甲乙為黃道丙丁為黃道極過此二極之赤道緯圈為丙己為戊丁名南北極圈
《與「地平圈」 比論》,
黃道與地平相遇作角,其角隨時隨地大小不同,正 偏球皆然,平球則否。
《與地平南北圈比論》,
兩圈交而作角,自六十六度有奇而至九十,九十為 二至,則直角;六十六為二分,則銳角。
論「本天之運動」,〈凡四章。〉
《總論》:〈凡一條:〉
《宗》動天常,平行終古,無遲疾,赤道繫焉,故其行亦終。
圖
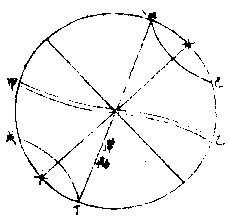
古無遲疾
諸點與地平比論〈凡十八條〉
凡先在地平下不見後見在地平上為出反是為入凡平球各點見地平上者皆與地平平行無出入七政則否
如上圖甲乙為地平與赤
圖
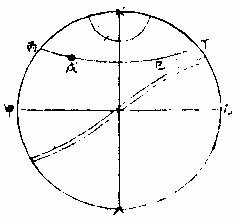
道同線丙丁等為距等圈凡戊己等點皆與地平甲乙平行獨七政循黃道行則否
若黃道極在天頂則黃道每日一次與地平為一線一瞬則六宮在地平上六宮在地平下矣此非圖像可明視渾球則得之離黃
道極圈而外,則出入皆有法。一宮先出,二宮繼之,入 亦然。若黃道極圈之內,赤道極之外,則反是。
欲測各點運行,視其出入於地平,測法必以赤道之 升度為其尺度也。何者?赤道恆平行,是名有法,是為 有准分之尺度故。
平球而外,凡各宮出地平上,在黃道俱三十度,赤道 則有長短。測法俱不用黃道之長度,而用赤道上之 黃道升度。
如北極出地十度為丙乙,其黃道初宮出地為丁戊。
圖

三十度則截取赤道先與黃道初度同出今與黃道第三十度同在地平線上者為己戊得二十四度弱是為黃道初宮之地升度凡論時刻及各點出入皆用之不用丁戊也
凡測升度有二或連或斷連者俱初宮初度起至本
圖
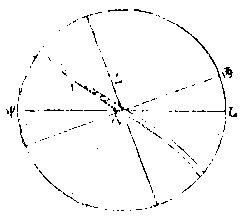
點依前法視赤道同出度即得若有別設二點在黃道上欲測二點之升度是為斷也法以前點視初宮相距之升度幾何是為前升度以後點距初宮之升度幾何是為總升度於總升度中減去前升度即得後升度
如右圖乙甲為別設點,求其升度,則丙乙為戊丁之升度,是前升度。戊甲為丙甲之升度,是總升度。次於 戊甲減戊丁,所存丁甲是乙甲之後升度。
問:「黃道弧而用赤道之升度,為其不等故也?亦有等 者乎?」曰:「有之。論正球則黃赤道從二分二至起算,各 出地九十度。其黃道弧與升度等,周天之中,其相等 者四而已。」
問:「正球黃赤道之四象限,其升度與弧俱等者何故?」 曰:「黃赤道俱為二大圈相等,則所分之相似圈分俱 等,一也。又極至極分二大圈,定黃赤道為四象限,此 二大圈出入地時,即地平與四象限之交相合為一 線,故黃道之象限交,必與赤道之象限交,偕出偕入, 二也。」
若欹球,則黃道之半圈,從分起、從分止,與赤道升降 度等;而周天之中,其相等者二。何者?黃赤道二分之 交,同時至地平,即二大半圈,必相等故。
欹球二相等之外,其他升度與黃道弧皆不等。 問:「二象限同升常自不等,何以至九十度則等?」曰:黃
圖

道弧與升度從初宮初度始每度之升度各有差初差漸多後差漸少漸近漸少至極遠而平故也過二至則反是
若正球則四象限之黃道弧與升度常相似其差甚少不過三度欹球則所差絕多
圖

如正球甲乙赤道軸即地平故丁丙弧與丁戊升度相似欹球北極面則辛壬弧與辛癸升度所差多升降有二有正升降有斜升降各弧與升度同出入若赤道上升度大於黃道弧謂之正升降小者謂之斜升降愈大愈正為黃道
與地平為角,近於直角,愈小愈斜為遠於直角。 《正球》但有四宮為正升,冬夏至前後各二宮是也。冬 至先後者,析木星紀。夏至前後者,實沈鶉首。餘八宮 有斜者,有半斜者。
若《欹球》,則恆有六宮為正升。正升謂之「遲升」,斜升謂 之「疾升。」欹球有六宮焉,正球有八宮焉。
問:「欹球之正升者六,為何宮?」曰:「若北極出地一度至 六十六度,則鶉首、鶉火、鶉尾、壽星、大火、析木是也。此 六宮則正升,正升則斜降。南極出地者反是。」
球愈欹,則黃道與地平,為角亦愈斜。
以《升降比》論。〈凡四條:〉
論「正球黃道上兩點去離二至二分」,〈亦名為四大點〉各等,則 其升度亦等。
其相對之宮,升度亦等,如「降婁壽星各二十七」之類 是也。
若《欹球》,則相對宮之升度各不等;
有兩點,去春秋分大點等,則其升度亦等。
《以正欹球比》論。〈凡二條:〉
從降婁至鶉尾六宮,欹球之升,度小而正,球大。從壽 星至娵訾六宮反是。
有兩弧在黃道上相對相等,其正球之兩升度並為 一率,欹球之兩升度並為一率,此兩率等。
以《黃道》之《出入比》論。〈即「升降度」 之「合」 也,凡五條。〉
各宮各弧各點之出度,必等於入度。〈不論正偏球〉 各宮之出入度,並與相對宮之出入度並等。
欹球各宮之出入度雖等,而正斜不等,此正升則彼 斜降,此斜升則彼正降。
圖
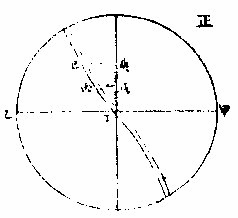
一宮一弧在正球有升度在欹球有升度此兩升度相減之較名升差
如上圖降婁一宮在正球之地升度二十六為甲乙北極出地四十度之欹球地升度十六為丁己此二率相減得十度是為兩球升度之差〈省曰升差〉
正球之升降度,從地平起算可;從地平南北圈起算 亦可。為赤道。與地平圈與南北圈相遇,俱為直角。故 《等欹球》則否,必用地平也。
《太陽篇》第四:〈不稱「日」 者,《篇》中有「時日」 之日,故別言之。月稱、「太陰」 同。〉《總論》:
宗,動天之下,則有列宿,又下則填星,則歲星,則熒惑。 何以序先太陽?其義有三:一、列宿與六曜之理,皆繫 太陽,不先論此,不得論彼;二、理較易,明,先明其易,難 者並易。三萬光之原,諸曜皆從受光焉。月若其配,星其從也。
從《本體論》。〈凡三章。〉
《論太陽之形象本是圓體》,
「圓,有面有體。太陽之為圓面,舉目即是,不待言矣。其 為圓體,何從知之?」曰:「凡物未有有面無體者,太陽之 為物大矣,知其必有體也。凡自然生者,初生者無物 不圓。太陽之生,亦本自然,曾無雕琢,初生則然,曾無 遷變。又諸體中,圓為最尊,以太陽較天下有形之物 亦是最尊,知其必為圓體也。」
圖
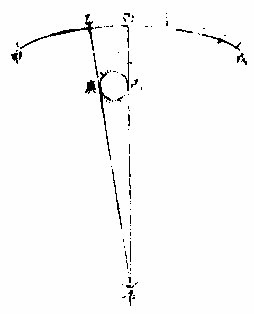
論太陽之大
欲知物大先知其徑徑有二一為視徑視徑者人目所視也舊云太陽之徑一度近來測驗實止半度如上圖甲乙乙丁丁戊為宗動天內規面之三度人從辛視太陽之己庚徑於天度僅得丙丁不滿乙丁
圖

之一度約如乙丙者七百二十則滿黃道周故知視徑為半度也
一為本徑欲知本徑先論其去地之遠太陽去地有時近有時遠折取中數則以地全徑為度
里數太多難計故以地徑之里數為其尺度也
地之周約九萬里,其全徑約三萬里。
「二十四,其地徑自之」,得五百七十六,是太陽去地之 中數也。
其《比例》云:「地之徑與太陽去地之半徑若一與五百七十六也。」
既知其視徑,又得其去地之遠。因以《割圓術》求其本 徑,得太陽之容,大於地之容一百餘倍也。
割圓術有專書,二徑,相比見幾何原本第十二卷第十八題容者體之容,算術謂之立圓積,非徑線。
圖
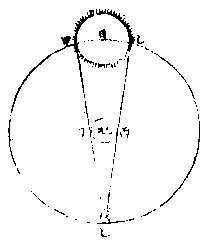
亦非面也其算法後篇詳之
論太陽之光
日為大光六合之內無微不照有不透明之物隔之則生影地在天中體小於日故影漸遠漸殺以至於盡其影之長不至太陽之衝
如右圖,甲乙為日,丙丁圈為地,其影至戊而止,不至 己。
太陽面上有黑子,或一或二,或三四而止,或大或小, 恆於太陽東西徑上行,其道止一線,行十四日而盡。 前者盡則後者繼之,其大者能減太陽之光。先時或 疑為金水二星,考其躔度則又不合。近有《望遠鏡》,乃 知其體不與日體為一,又不若雲霞之去日極遠,特 在其面而不審為何物。
從《運動論》。〈凡五章。〉
「太陽之動有二:其一與《黃赤道比論》,其一與《地平比 論》,與《黃赤道比論》。如從冬至一點起算,行天一日一 周,明日不在冬至,即此一圈作螺旋一周,次日復然, 迄夏至點行一百八十餘周,而通作一螺旋線也。第 冬至線與次日一周線相離甚近,以次漸遠,迄春分 而甚遠,過此漸近,迄夏至而甚近,過此又漸遠。如是」 循環無窮耳。詳見後篇。
又冬至初日之線,其螺圈甚小,次日漸大,至春分甚 大;過此漸小,迄夏至而甚小。如是小大循環者,何也? 為緯圈中冬、夏至皆小圈,赤道為大圈故也。從冬至 迄夏至,此為成歲之半矣。若從夏至迄冬至,亦作螺 旋行,每日一周百八十餘日,通作一螺旋線。但此線 非復前線,而別作一線,每日與前線作一交耳。此為 成歲之全也。
圖
其意。已上所說螺旋線,是太陽之體理,實作如是運 動,無可疑者。但螺旋則無法之線也,以此測候,亦復 無法可立,故天官家別用他術如下文。
測候之術
如用「春分起算,初日從初點循赤道行迄一周,是為 一日。明日即不在赤道,而在其第二圈,又不直距於 初點,而東西相去為黃道之一長度,其南北距度即 不及一度也。此一周即為赤道之一距等圈矣。太陽 恆在黃道下行,故無黃道之廣度。」至第三日,復作第 三距等圈,與次日同。凡九十日,行黃道九十度,即於 赤道旁作九十距等圈。其第九十則夏至圈,夏至圈 去春分圈止二十三度半,故太陽之行亦如是而止。 此九十距等線以當全螺線之半也。用此術則從夏 至迄秋分亦有九十距等線,其線即春夏距等之原 線矣。
至秋分即復行赤道,一日無距度,距圈與前春分日 所行同線相對,其兩對處則有極分交圈以為之限 也。自春迄秋,二分之間,行一百八十度,黃道長度與 赤道之距度其數皆等。從秋分而後,每日作一距等 圈。其第九十則冬至圈也。凡諸距度圈皆交於黃道, 獨二至之兩圈切於黃道,為其行至是盡矣。其兩盡 處,則極至交圈為之限也。秋分迄冬至,亦二十三度 半,與其迄夏至等,故其間距等圈與其迄夏至之距 等圈亦等。從冬至以後,亦依前所行距等原線,以迄 春分而歲成矣。
「太陽之行恆在黃道下,無廣度,亦恆在兩至之內。故 兩至之內,皆為太陽所行之道,而太陽每日行一度 弱,故兩至間之距等圈,凡一百八十二有奇,每一圈 歲兩經焉。」如此術即分太陽所行為二路。其一,分計 每日所行,各行於赤道侶圈,皆在兩赤道極間;其二, 總計每歲所行皆行於黃道,在兩黃道極間。其一日 一周,於黃道為一長度;於赤道上不及一上度,此一 上度弱者,名為「黃道一日之升度。」黃道之升度,每宮 與赤道不等,故每日黃道之升度,一一不等。〈見本設表〉
《螺旋合術》與《黃赤分術比論》
論《合術》則自東而西,每日不及一度,故云「日遲。」論分 術則自西而東,每日循黃道行一度,故云「日疾。」其實 一也。但螺旋於理甚合,而無法可推;分術則分數易 明,其間即有參差,不能及一微一纖,非儀象可測;故 曆家專用分術。〈加減法也〉以便推步。
與地平比論
太陽至地平上,為出,為明;從東而西,沒於地平下,為 入,為晦。
論正球春分日,太陽出於東方,行赤道,赤道即東西 圈,漸升至頂,極至南北圈,為極高之弧。此地平以上 之半晝分也,亦謂之「東半晝弧。」午正後漸降至地平, 謂之西半晝弧。東西合為全弧,行盡全弧為一晝。 其一日之中,地平上凡有表即得影,日出則為無窮 之西影,漸短至頂,僅得一點。
或云:「是為無影,安得一點?」 不知無表即無影,若令表離於地平,即有與表等大之影。
午正後,影漸長,至地平,復為無窮之東影。日既入地 平下則有朦朧分。〈一名昏度一名黃昏〉行地平之低度,十八。
圖

低度者非黃道赤道之度乃地平之緯度也在下名低度在上名高度
後此為夜
如上圖甲乙為赤道即東西圈丙甲丁為南北圈甲之高九十度滿一象限己戊為表日出辛表端影在庚至壬影在癸至庚則在
辛也,至甲止一點,丙丁即地平低度,十八至子丑而 止矣。
日至於南北圈下,為半夜迨,近地平下十八低度,復 為朦朧分。
一名《晨度》,一名昧旦,一名黎明,一名《昧爽》。
凡黎明將盡,日將出,地平上有雲,則為朝霞。黃昏之 始,日初入地平上有雲,則為晚霞。所以赤色者,為日 光返照,如火出煙。本是黑色,與火並見,即黑見煙,不 見火,即為紅煙矣。
問:「日出入則大,日中則小,何故?」曰:「地居天中,日周其 外,因於太陽,如受燔炙,恆出熱氣,是名清蒙之氣。此 氣之厚,去地不能甚遠。日出入時,人目衡視積氣甚 多,如物在水中,其體大於本體,故出入時,日形似大, 非果大也。至日中時,以垂線照地,人直視之,積氣甚 少,日不受蒙,則似小矣。若出入時,或深紫,或微紅,或」 似長圓,亦皆是氣之厚薄疏密所為也。
其春分,次日,太陽離赤道,即不出於東西圈之初度, 而在其稍北之闊度。〈即地平之經度不言廣者以別于黃道緯度也〉其相去也與其日之距度等。〈為正球則赤道與地平為直角故也欹球則否〉太陽既 稍北,則其表影亦稍南,其晝分與初日等。其南北圈 下之極高弧,則稍減於九十度。又次日則闊度愈大, 極高弧愈小。以迄夏至,其闊為二十三度有奇,其高 弧為六十三度有奇。從赤道南迄冬至,亦如之。其方 之晝與夜恆等。何者?赤道與地平為直角,即一切經 緯圈,其隱見恆相半故。
如左圖,甲乙為赤道,即東西圈,春分日,日從此道行, 次日以後,漸向丁戊行,甲至丁、乙至戊各二十三度。
圖

有奇庚至丁其高弧六十三度有奇
論欹球一歲中獨春秋分兩日得晝夜平何者是其日太陽在赤道下赤道與地平皆大圈交而相分即所分之圈分相等若赤道距等圈大小不等以地平分之其圈分上下皆不等
圖
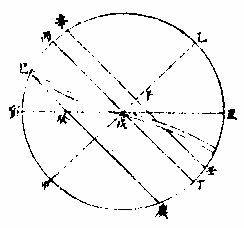
如上圖甲乙為南北極丙丁為赤道丑寅為地平春秋分兩日日在戊為黃赤道之交則地平上下圈分等過春分日漸北如至辛壬距等圈則丑寅地平分晝夜於子過秋分日漸南如至己庚距等圈則地平分晝夜於癸上下皆不等
又一歲之中,凡兩晝之距、兩至等,則其晝分之長短 亦等。凡兩晝之距、兩分等,即一在赤道南,一在赤道 北,其距度等,而此日之晝與彼日之夜等。
凡球愈欹極,愈高即高至。〈不曰冬夏至而曰高至通南北言之〉之日愈 長。
凡正球之南北闊度等,欹球則否。
凡正球之二至日中時,其高下恆相等;欹球,則否。日 中時,其二至,一甚高、一甚低。
論平球,則以半年為一晝,以半年為一夜。何者?北極 與頂極合,即赤道與地平亦合。故九十距等圈,從赤 道迄一至,皆在地平上,其在下亦如之也。其表恆作 無窮,及最長影不作短影。每日為一周,亦作十二時 或二十四,但百八十周恆在晝耳。
論朦朧
早為晨分,暮為昏分,或並曰「晨昏」 ,或省曰「朦」 ,曰「朦影」 、朦度。
太陽在二點,二點之距一至等,其朦亦等,何者?去至 等則同在一距等圈上故。
若二點之距一分等,其朦不等,孰大孰小?近於上極 者則大,遠則小。
北極出地處,則北六宮之朦大於南六宮,南極出地 處反是。
北極出地處,太陽在北六宮愈近夏至,朦愈大,迄夏 至極大,過夏至漸小。南方近冬至愈大,迄冬至則極 大,過冬至漸小。北極出地處迄冬至不極小,極小者, 在赤道冬至之間。南方迄夏至不極小,極小者,在赤 道夏至之間。
太陽在北六宮,愈北朦愈大。
平球之處,其太陽入地低度不過二十三,去朦度之 十八未遠也。故其晨昏最長。一年之中,明多於晦,幾 乎不夜。
正球上兩點,在赤道南北,其距赤道等,其朦亦等;其 距赤道不等,其朦亦不等。孰大?愈遠赤道者愈大,故 「二至之朦甚大,二分之朦甚小。」
問:「欹球北極出地處之朦,夏至極大,而冬至不極小, 極小者在赤道冬至之間,然則安在?」曰:「此在秋分之 後,特隨地不同,皆在分後至前,不在其日也。如北極 出地四十度,春分則六刻三十三分,夏至八刻六十 分,秋分六刻三十三分,冬至則七刻,最小者六刻二 十六分有奇,在寒露之中,候五日也。」〈有本表〉
太陰篇第五
五緯在二曜之上,今先太陰者何故?一、凡論年月日 時,皆以二曜定之。二、其理較五緯特為易明。三,太陰 體大,晝時亦見;四、太陰之能力亞於太陽,五緯無能 及之。
從本體論
論太陰之形象本是圓體,與太陽同,雖有晦朔弦朢, 不害為圓,詳見《後論》。
論太陰之大「太陰去人時近時遠,折取中數八,其地 半徑自之,得六十四半,徑為三十二全徑」,是太陰去 地之中數也。
其視徑去人愈近愈大,愈遠愈小,折取中數,亦得半 度,與太陽等。
其本徑則小於地球地之容大於月約三十倍也
圖

論太陰之光本自無光受光於太陽故本球之光恆得半以上因太陽之體大於其體故
如上圖甲乙為日丙丁為月徑因日大故受光至於戊己
太陰面上黑象有二種其一今人人所見黑白異色
者是其二。小者則日日不同,非遠鏡不能見也。詳見 《後論》。
從運動論
太陰之運動有二:其一一日一周,隨宗動天行,與六 曜同公動也。其二「循白道。」〈白道月之本道一名月道下文通用〉日行十 三度有奇,迄二十七日有奇,而一周。本動也。因太陽 同行二十七日有奇,則過周二十七度有奇,故又二 日有奇,乃及於日而與之會。
白道不與黃道同線,而兩交於黃道。
兩交名「正交、中交」 ,亦名「天首、天尾」 ,亦名「龍頭、龍尾」 ,亦名「羅計。」
兩半交去黃道五度有奇,故每行一周。在黃道下者, 二交初、交中是也。他詳後論。
《時篇》第六:〈凡十三條。〉
既明二曜之體,又明二曜之運次,因其運動以得時。 時者何物?凡諸有形之物,必有變革,變革多端,中有 遷運一端,因其遷運先後,從而測量剖分之,則為時 也。
問:「草木鳥獸人事,皆有變革遷運,亦可用以為時,何 必二曜?」曰:「凡立術有三法:一須公共,一須分明,一須 永久。惟二曜則然,他無有足比者故也。」
時之準分尺度一日是也。一日者何。太陽行一周而 過赤道。上之一升度弱。〈當黃道一度〉者是也。「日之起算有 四法,或以早,或以晚,或以晝之中,或以夜之中。 日有大小分,大者為晝夜,小者為時辰。時辰者,十二 分日之一也。」〈西曆為二十四分之一〉
常靜天之上有二大圈,皆過兩極,而分赤道為四平 分:其一過頂即子午圈,其一過東西點。
「東西點」 者,赤道交於地平,是東西之最中。
即「卯酉圈,從卯至午,其間又有二圈,為辰為己。從午 至酉,其間又有二圈,為未為申。此六圈者,終古不動。 凡三曜至某圈上,即為某時也。」
「十二時辰」 ,不止日也。月所至,即為月之十二時,星所至,即為星之十二時。
其起算亦有四法:或用子,或用午,或用卯,或用酉。 時又有刻,每時八刻,一日則九十六刻。東西所同用 星,官家用百刻,取整數易算也。
刻又析為百分,分析為百秒逓為百以至微。西法每 刻為十五分,分析為六十秒逓分之皆以六十也。 其積日者,以日加之,初加為一旬。一旬者,甲至癸十 日,再加為一月。一月者,太陰行一周而與日會也。
稱「一月」 者有二義:一為二十七日有奇而周於天,一為二十九日有奇而及於日。因交會之理分明,故不用月周,而用朔實也。
月之分也,兩分之為朔朢,四分之為晦朔。弦朢 太陽行一周,三百六十五日四分日之一弱為一歲, 謂之「太陽年。」其起算亦有四法:一從冬至,一從春分。 〈測天用之〉一從秋分。〈論二十八宿起於角亢在秋分後〉一從夏至。〈古時或用之〉 「用太陽年」者,四年而閏,一日為四分之一也。四百年 而減一閏,為弱也。
凡論歲,以太陽為法。太陰行十二周為一歲者,為其 近於太陽年也,是謂之「太陰年。」用太陰年者,歲積氣 盈朔虛,十日有奇。三年一閏為十日,故五年再閏,十 九年七閏為有奇,故
太陽年之分也。二分之為半歲周,四分之為四季,八 分之為分至啟閉。〈立春立夏為啟立秋立冬為閉〉十二分之為節,二 十四分之為節,氣中氣,七十二分之為候,
其積年者,以年加之,十二年為一紀,三十年為一世, 六十年亦為一紀。
恆星篇第七
向己說常靜宗動二天,二天之下,則恆星天也。略論 其凡有四,其一為幾何,其二為貌狀,其三為能力,其 四為遷變。
幾何?〈凡六條:〉
萬物中,《形天》為最大。大有二義:一、在上所最遠,故最 大;二、能力最大,故其體亦大。
「其形象為圓球」,何以知之?天體最為精純無雜,最為 單獨無二。圓之為象,亦無雜,亦無二,體性如此,故其 形象亦當如此。又運行最疾者,莫如圓體,他體則滯 礙也。
「其去地最遠遠之數,以地之半徑為度,最近處得一 萬四千度」,自此以上,非人思力所及知也,此端似為難信,證見後篇。
其所在,萬物之最上。
其質最細。何以徵之。常在上不霣墜。知為輕虛細密 也。其質又極精純。為無他夾雜故。
貌狀。〈凡一條:〉
天下之物,皆以顏色為其美飾。顏色之外,別有二美 飾,一為透徹,一為光耀也。顏色之美,美之下分;明光 之美,美之上分。何者?其形妙好,異於他色,一也;人之 見之,無不喜悅,二也;他物不能自見其美,惟光能自 見,三也;他物有色,惟光能發揚其美妙,四也。有此四 者,故為天下真寶。天最尊於萬物,故一切顏色不足 為其文飾,惟光為其飾矣。或云:「天望之蒼蒼。然蒼非 色耶?何謂無色?」曰:「蒼蒼非色也。太空之中,氣盈其處, 氣亦無色,氣積極厚,則成蒼蒼之色。譬之玻璃,本自 透明,略無他色,積之數重,則成蒼色。太空中色,亦猶 此耳。」
能力。〈凡四條:〉
「天之《下濟》,其於下土」有大能力。何以徵之?運行一周, 成為四季,涼燠寒暑,萬物藉為生長收藏,一也。世間 微物,無不各有能力,稍大則能力稱之天,如彼其大 也,知其能力與之等大,二也。
天之能力,下及每用二器,其一,光也;其一,施也。光不 獨能照天下,亦能作熱。如用窪鏡對日而成返照,則 能生火。又用玻璃圓球對日而成折照,亦能出火。其 故為何?「光於天下為最尊,熱於四大物情中。」〈四大情者一熱 二冷三燥四濕〉「亦為最尊。」「以尊生尊」,是其理也。其次亦能生 冷,亦能生燥,亦能生濕。為光本非熱非冷。非燥非濕。 而其中有精,足當四情。故能生熱、生冷、生燥、生濕也。
如仁中無芽葉花實,而其精足當四物,故能生「四物」 也。
夫光之為體。若其發而及物。何為施之不盡。若其不 發。則一切所受,為從何來。故其體其用。總非人間意 量所及。
光之外,別有施者,不屬光也。此有二證:其一,海潮大 小,不因於光,亦不因於冷熱燥濕。譬如磁石吸鐵,別 有相攝相受者,則受者為所施,攝者為能施也。又如 懷胎生子,七月生則長,八月生則殀,無不驗者。此亦 非因於光,亦非因於四情,亦如磁鐵,有別相攝受者 故也。
從上二能,知「天於下土」,蓋有四德:一曰覆冒,一曰包 函,一曰生育,一曰保存也。假令不動,亦有此德,而又 加之運動,於此若此,於彼若彼,變化無端,真非思議 所及矣。
遷變。〈凡四條:〉
凡物遷變首運動,
天之運動皆環行,何者?天體單獨無二,故其運動,亦 應單獨無二。「環行」者,單獨無二之行也。何謂「單行?」曰: 凡動如人、如鳥獸、如風,皆雜亂無法之行也。單行有 二:一曰垂線,一曰圓線。石在空中下墜於地,此為垂 線。一切循環無端者,皆為圓線。垂線之動,勢盡而止。 惟圓線獨為無窮。天以覆函生存下土者也,故不能 不為無窮,不能不為《環行》矣。
天之運動,恆不去其本所論其各分無一不動,而其 全體無一分動。
天之運動有四異:其一甚疾,一刻分中行幾萬里,如 鳥,如矢、如砲、如霹靂,皆非所及;其二恆平行。
其中遲速,別有故實,無一不平行者,詳見後論。
若非一一平行,即測候之術無從可用;其三,「恆久不 已;其四,萬物之動此為首。何者?天下之動,於此繫焉 故也。若無此動,即無四季,即無生物。」問:「運動而外,更 有遷變乎?」曰:「論其體則無變,何者為在最上物無及 其際者,故不能受變於物。論其情則有變。如月星無 光,因於日光變而有光,一也;又如日月有光,因於交」 食,而若無光,二也。〈以上原本卷下。〉
Public domainPublic domainfalsefalse
![]()
本作品原文沒有標點。標點是人工智能程序古詩文斷句 v2.1創建,並且經由維基文庫用戶編輯改善的。本站用戶之編輯以知识共享 署名-相同方式共享 4.0协议(CC BY-SA 4.0)發佈。
歡迎各位持續修正標點,請勿複製與本站版權協議不兼容的標點創作。
![]()
Public domainPublic domainfalsefalse