| 欽定古今圖書集成 曆象彙編 第一百五卷 |
欽定古今圖書集成曆象彙編曆法典
第一百五卷目錄
測量部彙考六
新法曆書三〈測天約說上〉
曆法典第一百五卷
測量部彙考六
编辑《新法曆書三》
编辑
測天約說上
编辑「測天者,修曆之首務;約說者,議曆之初言也。不從測 候,無緣推算,故測量亟矣。即測候推算,亦非甚難不 可幾及之事。所難者,其數曲而繁,其情密而隱耳。欲 御其繁曲,宜自簡者始;欲窮其隱密,宜自顯者始。」約 說之義,則總曆家之大指,先為簡顯之說。大指既明, 即後來所作《易》言易知,漸次加詳,如車向康莊,此為 發軔已。又古之造曆者,不欲求明,抑將晦之,諸凡名 義,故為隱語。諸凡作法,多未及究論其所從來,與其 所以然之故,牆宇既峻,經途斯狹,後來學者,多不得 其門而入矣。此篇雖云率略,皆從根源起義,向後因 象立法,因法論義,亦復稱之,務期人人可明,人人可 能,人人可改而止,是其與古昔異也。或云「諸天之說, 無從考證,以為疑義。」不知曆家立此諸名,皆為度數 言之也。一切遠近、內外、遲速、合離,皆測候所得,舍此 即推步之法,無從可用,非能妄作,安所置其疑信乎? 若夫位置形模,實然實不然,則天載幽元,人靈淺尟, 誰能定之?姑論而不議可矣。都為二卷,共八篇如左。
首篇
度數之學,凡有七種,共相連綴,初為二本:曰數,曰度。 數者,論物幾何,眾其用之,則算法也。度者,論物幾何, 大其用之,則測法、量法也。
測法與「量法」 不異,但近小之物,尋尺可度者謂之「量法。」 遠而山岳,又遠而天象,非尋尺可度,以儀象測知之,謂之「測法。」 其量法如算家之專術,其測法如算家之綴術也。
「既有二本,因生三幹:一曰視,人目所見,一曰聽,人耳 所聞,一曰輕重,人手所揣。耳所聞者,因生樂器樂音。 手所揣者,因生舉運之器。舉運之法,惟目視一幹,又 生二枝:一曰測天,一曰測地。」七者在西土庠士俱有 耑書。今翻譯未廣,僅有幾何原本一種,或多未見未 習。然欲略舉測天之理與法,而不言此理此法,即說 者無所措其辭,聽者無所施其悟矣。七者之中,音樂 與輕重別為二家,故茲所陳,特舉其四:曰「數」,曰「測量」, 曰「視」,曰「測地。」四學之中,又每舉其一二,為卷中所必 需。其餘未及縷悉者,俟他日續成之也。為他篇所共 賴,故列於篇次之外,曰「首篇。」欲知他篇,須知此篇,故 又名《須知篇》。
數學一題
「比例」者,以兩數相比,論其幾何。
比例有二:一曰相等之比例,一曰不等之比例。若二 數相等,以此較彼無餘分,名曰「等比例」也。若二數不 等,又有二:一曰以大不等,一曰「以小不等。」如以四與 二相比,四之中凡為二者二,是為以大,即命曰「二倍 大」之比例也。如以二與四相比,倍其身乃得為四,是 為以小,即命曰「二分之一」之比例,或命曰「半比例」也。
測量學十八題
第一題至第十四題,《論測量之理》。
《第十五題至第十八題,論測量之法》:
幾何原本書中,論線、論面、論體。今第一以至第五,論 線也。第六以至第十四,論體也。此書中不及面,故不 論面。
《幾何原本》書中多言直線、圜線,其理易明,今不及論。 論其稍異者有五題,前二題言獨線,後三題言兩線。
第一題:〈獨線一。〉
長圓形者,一線作圈,而首至尾之徑大於腰間徑,亦 名曰《瘦圈界》,亦名《撱圈》。
如甲乙丙丁圈形,甲丙與乙丁兩徑等,即成圈。今甲 首至丙尾之徑,大於己至庚之腰間徑,是名長圓。 或問此形何從生?答曰:「如一長圓柱,橫斷之,其斷處。」
圖

為兩面皆圓形若斷處稍斜其兩面必稍長愈斜愈長或稱卵形亦近似然卵兩端小大不等非其類也
指其面曰平長圓若成體曰立長圓
第二題〈獨線三〉
蛇蟠線者於平面上作一線自內至外恆平行恆為
圖

圈線而不遇不盡如上圖自甲至乙者是
旋風線者於平圓柱上作一線亦如蛇蟠但蜿蜒騰凌而上如旋風也
如上圖自甲至乙者是螺旋線者於球上從腰至頂作一線如蛇蟠而漸高如旋風而漸小
如右圖自「甲」至乙者是。
此書獨用《螺旋線》,欲解其形勢,故備言之。
第三題
下三題言《二線》者,或直,或不直。或相遇,或相離。
二線相遇者有三:但相遇而止,名曰「至線」;因至線在 所至線之上,故又曰「在上。」其割截而過者,名曰「交線」, 亦曰「割線」,亦曰「截線」;其至而不過又不止者,名曰「切 線」;其至線而有所分截者,亦稱「割線」,或曰「截線」,或曰 「分線。」
圖

如上圖甲乙線與丙乙丁線丙乙丁圈相遇至乙而止則甲乙為至線又曰丙乙丁上線
如上三圖甲乙線截丙丁線於戊己庚線截辛壬癸圈於辛子丑寅圈截丑卯寅圈於丑於寅皆謂之曰交線
圖

又如上圖甲乙線遇丙丁圈於丙戊己庚圈遇戊辛壬圈於戊皆名之曰切線也
如上圖甲丙線分甲乙丙圈者曰分圈線亦曰割圈線亦曰截圈
第四題
兩線不相遇而相離之度
圖
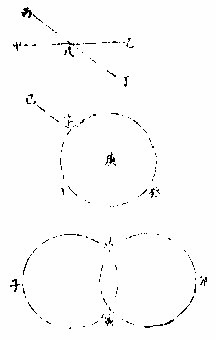
恆等名曰距等線
或稱平行線侶線俱通用
如上三圖甲至己乙至戊丙至丁其相離之度俱等
第五題
兩線相遇即作角
本是一面為兩線所限限以內即成角也
圖
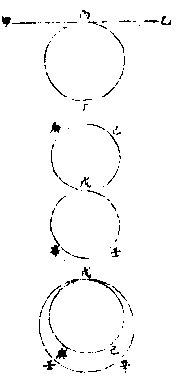
如上圖甲乙與乙丙兩線相遇於乙即包一甲乙丙角〈第二字即所指角〉其球上兩圈線相交,亦作角。
如上圖甲丙乙丁兩線交而相分於戊即成甲成丁丁戊丙丙戊乙乙戊甲四球上角也
第六題
自此至第十四題皆論體。諸體中「球」為第一。此書所 用,獨有球體,故未他及。
凡物之圓者,皆名「球。」 諸題中名義,凡立圓物皆有之,非獨天也。
第《六至第八,言球內之理》;第《九至第十四,言球外之 理》。
球之內有心心者,從此引出線至球面,俱相等。 如左圖:甲乙丙球,丁為心,從丁引出線至甲,至乙至
圖
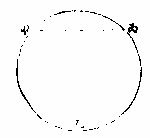
丙各等即作百千萬線皆等
第七題〈球內〉
徑者一直線過球心兩端各至面半徑者從心至面如上圖甲乙球丙為心一直線過丙兩端至甲至乙即甲乙為徑線其丙乙丙甲皆為半徑線
圖

第八題〈球內〉
球不離於本所而能旋轉則其一徑之不動者名為軸軸之兩端名為兩極也凡一球止有一心凡球之轉止有一軸其徑甚多無數可盡
如上圖甲乙丙丁球戊為心乙丁過心此球從甲向
丙丙又向甲旋轉而不離其處,則乙戊丁直線為不動之處,是名軸也。乙與丁則為兩極球心,若離於戊 點如己,則從心所出兩半徑線如庚己,己辛必不等, 故曰「止有此心。」凡軸皆利轉,若有二軸,二俱轉即相 礙,一不轉即非軸,故曰「止有一軸。從心出直線。」苟至 面皆徑也,故曰「無數。」
《第九題》:〈球外:〉
球之面可作多圈,圈有大有小,大圈者,其心即球心, 若從圈剖球為二,則其圈之徑過球心也。各大圈從
圖

圈面作垂線各有其本圈之軸與其兩極
如上圖甲乙丙丁球上作甲戊丙己大圈其垂線乙丁即乙丁為本圈之軸乙丁兩點即其兩極故大圈在兩極之間離兩極俱相等
第十題〈球外〉
圖

小圈者不分球為兩平分不與球同心其去兩極一近一遠愈近所向極愈小愈近心愈大
如上圖甲乙為大圈丙丁戊己庚皆小圈也故一大圈之上之下可作無數小圈眾小圈之間止可作一大圈
第十一題:〈球外:〉
圈不論大小,其分之有三等。
「三等」者,一曰大分,一曰小分,一曰細分。如兩平分之 為半圈,四平分之為象限,此大分也。每象限分為九 十度,此小分也。每度又析為百分,每分為百秒,遞析 為百至纖而止。《西曆》則每度析為六十分,每分為六 十秒,遞析為六十至十位而止,此細分也。
第十二題:〈球外:〉
兩大圈交而相分為角。欲測其角之大從交數兩弧。
圖

各九十度而遇過極之圈兩弧所容過極圈之弧度分即命為本角之度分如上圖戊丁乙為過極圈有甲乙丙甲丁丙兩大圈交而相分於甲於丙問丁甲乙角為幾何度分之角法從甲交數各九十度而遇過極之戊丁乙圈為甲
丁甲乙此兩弧間所容過極圈之分,為丁乙弧。如丁 乙六十度,即命丁甲乙角為六十度角。
《第十三題》:〈球外:〉
凡大圈俱相等,兩大圈交而相分,其所分之圈分兩 俱相等。
凡大圈必於本球之腰。腰者,最大之線也。凡最大之 線止有一,不得有二,故展轉作無數大圈,俱相等。圈 既相等,則以大圈分大圈,其兩交線必在球之腰,此 交至彼交,必居球之半,故無數大圈各相分所分之。
圖

兩圈分各相等有不等者即小圈也
第十四題〈球外〉
大圈俱相等故所分之度分秒各所容皆相等小圈各不相等故度分秒之名數等其所容各不等如上圖甲乙己為大圈丙丁戊為小圈大圈既相等
即多作大圈,皆與甲、乙、己圈等,而各圈之甲至乙其 度皆等。若丙、丁、戊小圈既與甲、乙、己大圈不等,則甲 至乙與丙至丁同名為若干度,而所容之廣狹不等。
第十五題:〈以下四題,言測量之法。〉
長方面,其中任設一點,欲定其所在為何度分,作經 緯度求之。
法曰:先平分其長為若干度分,名經線。次平分其廣 為若干度分,名「緯線。」經與緯每度分之小大俱等。次 視經緯之線,其過點各若干度分,即命為點所在之。
圖

度分
如上圖甲乙丙丁長方形欲知戊點所在先從乙向丙作距等經線次從乙向甲作距等緯線次視戊點在經緯線之交為是何度即命曰在經度之四緯度之八也
乙至丙丙點得命為第
六、乙點,不得命為第一,而命為初,曆家言「算外」 者俱準此。
第十六題
其在球也亦如之。球之中任設一點,欲定其所在為 何度分,亦先作球之經度。
法曰:先於兩極之間作一大圈,為腰圈,平分腰圈為 三百六十度,從各度各作一過極大圈,即半圈平分 為一百八十度,是為腰圈上之經度。
如左圖甲乙丙丁球乙丁為兩極,於其間,作甲戊丙。
圖

己腰圈從戊向丙丙向己各作過極大圈即乙庚丁乙辛丁等線皆腰圈上之經度
第十七題
次作球之緯度即定所設點在何度分
腰圈之兩旁有兩極從腰圈向極分為九十度每度
圖
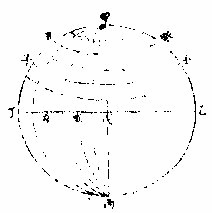
各作一距等小圈漸遠腰漸小至極而為一點即第九十小圈也次視經緯兩線之交命在設點在何度分
如圖甲乙丙丁球上依前題既作甲庚丙甲辛丙各經線次於乙戊丁腰圈上向甲極分為九十度每度
各作一距等小圈,如壬子、癸丑之類,皆緯圈也。次視 經緯各遇點之交,從腰圈線考其經度,從過極線考 其緯度,即命所設己點在從戊向丁之第四經圈,從 戊向甲之第三緯圈。
凡言「度」者,各有二義。其一,一度之廣能包一度之地, 是其容也。其一,自此度至彼度,各以一點為界,是其 限也。《腰圈度》之容,以各過極度之線限之,過極度之 容,以各距等線限之。
凡圈互相為經,亦互相為緯。如以過極為經,則距等 為緯,若以距等為經,則過極為緯。如幾何原本之論, 線互相為直線互相為垂線也。
第十八題
《論緯圈以大圈為宗》,
過極經圈,皆大圈也,皆等距等線限之。諸度分之容, 亦等距等緯圈,皆小圈也,各不等。過極圈限之諸度 分之容,愈近極愈狹,至極而盡矣。故緯度之容,等於 經度者,獨有腰圈一線,獨有初度初分初秒之一率。 過此以上,無不狹也,故當以大圈為宗。大圈左右諸
圖
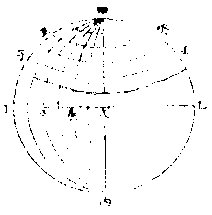
緯圈之上凡言經度之容者皆從此推減之圈愈小度愈狹即差愈多也
視學一題
凡物必有影影有等有大小有盡有不盡
不透光之物體前對光體後必有影焉若光體大於物體其影漸遠漸殺銳極
而盡。若光體小於物體,其影漸遠漸大,以至無窮。若 光物相等。其影亦相等亦無窮。
測地學四題
第一題
「地為圓體」,與海合為一球。
何以徵之?凡人任於一處向北行二日半,則北方之 星在子午線上者必高一度;次後二日半復高一度。 恆如是為相等之差。向南行亦如之。知從南至北為 圓體也。
圖

如上圖甲為北星丁為南星乙辛丙圈為地球人在乙則見甲正在其頂至戊則少一度矣從戊至己與乙至戊道里等又少一度矣迨至辛則不見甲至壬則反見丁安得非圓體乎若云地為平體則見星當如癸從丑向寅至辰宜常
「見不隱。」又丑至寅,寅至卯,若見子之高下所差等,則 道里宜不等。〈別有筭數〉「安得有時不見。」又恆為相等之差 也。
若人東行漸遠,則諸星出地者漸先見,西行漸遠漸 後見。故東西人見,日月食遲速先後各異,是知東西 必圓體也。
第二題
地在《大圜》,天之最中,
何以徵之?人任於所在見天星,半恆在上,半恆在下
圖
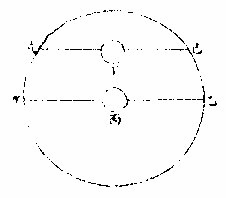
故知地在最中也
如上圖丙為地東見甲西見乙甲乙以上恆為天星之半知丙在中也若云非中當在丁則東望戊西望己當見天之小半而不見者大半
第三題
地之體恆不動
一、不去本所;二、亦不旋轉。云「不去本所」者,去即不在, 天之最中也。云在本所,又不旋轉者,若旋轉,人當覺 之,且不轉則已,轉須一日一周,其行至速。一切雲行 鳥飛,順行則遲,逆行則速。人或從地擲物空中,復歸 於地,不宜在其初所。今皆不然,足明地之不轉。
第四題
地球在天中止於一點,
何以徵之?人在地面,不論所在,仰視填星、歲星、熒惑, 彼此所見,恆是同度,故知地體較於天體,則為極小。
圖
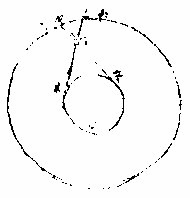
若地大者兩人相去絕遠其視三星彼此所見不宜同躔
如上圖丙己戊乙為天甲為地丁為星地體若大能為天分數者則人在庚宜見丁在己度人在辛宜見丁在戊度今不然者是地與天其小大無分數可論
也。
名義篇第一
《測天本義》,〈凡一條:〉
問:「測天者何事,所論者何義也?」曰:「此度數之學。度數 學有七支,此為第六也。所論者一言三曜。」〈日月星〉形象 大小之比例,一言其各去離地心地面各幾何,一言 其運動自相去離幾何,一言其躔離逆順、晦明朓朒, 一言其五相視。五相視者,一曰「會聚。」
《會聚》或同一宿,或同一宮,或相掩,或凌犯。
二曰《六合照》。〈每隔一宮〉三曰「隅照。」〈三方相望〉四曰「方照。」〈四方相望〉五 曰「對照。」〈即衝〉一、因其行度次舍,以定歲月日時,此為大 端也。
《大圜》名數:〈凡十條:〉
《大圜》者,上天下地之總名也。
亦稱「宇宙」 ,亦稱「天下」 ,亦稱六合之內,下文通用。
天實渾圓,其中毫無空隙。譬如蔥本,重重包裹,其分 數幾何,則自下數之。〈地居天中為最下亦曰最內〉第一為地水補 其闕。
「地有庳窪,水則就之,若據地面,則水土相半。」 蹠實論之,水之視地,僅當千分之一。
共為一球。地外為氣,氣之外為「《七政》之天」,七政之外 為恆星。〈亦曰經星下文通用〉「之天」,「恆星之外,為宗動之天」,「宗動 之外,為常靜之天。」
問:「地水與氣,相次之序,其理解易明。今何以知七政 在下,恆星在上?」曰:「有二驗焉:其一,六曜有時能掩恆 星。」
六曜者,月五星也。不言「日」 者,日大光星不可見也。唐肅宗上元元年五月癸丑,月掩昴。代宗大曆三年正月壬子,月掩畢;八月己未,月復掩畢。是月掩恆星也。唐高宗永徽三年正月丁亥,歲星掩太微上將;五月戊子,熒惑掩右執法。元武宗至大元年十二月戊寅,太白掩建星。是五緯掩恆星也。
「掩之」者在下,所掩者在上也。其二七政循黃道,行皆 速,恆星最遲也。
問:「七政中復有上下遠近否?」曰:「有之,月最近也。何以 知之?亦有二驗:其一能掩日五星也。」
月掩日而日為食,不待論也。唐文宗太和五年二月甲申,月掩熒惑。六年四月辛未,月掩填星於端門。九年六月庚寅,月掩歲星於太微。武宗會昌二年正月壬戌,月掩太白於羽林,是月掩五星也。
其二,循黃道行二十七日有奇而周天,餘皆一年以 上,是七政中為最速也。
問「行度遲速,以別遠近,是則然矣。太白辰星與日同 一歲而周,為無遠近乎?」曰:「舊說或云日內月外,相去 遼絕,不應空然無物,則當在日天之下;或云在日天 之上。二說皆疑,了無確據。若以相掩正之,則大光中 無復可見。論其行度,則三曜運旋,終古若一。兩術既 窮,故知從前所論,皆為臆說也。獨西方之國,近歲有」 度數名家,造為望遠之鏡,以測太白,則有時晦,有時 光滿,有時為上下弦計。太白附日而行,遠時僅得象 限之半,與月異理,因悟時在日上,故光滿而體微。
若地日星參直,則不可見,稍遠而猶在上,則若幾朢之月也。
《時在日下》則晦
《三》、「參直故晦,稍遠而猶在下若復蘇之月,體微而光燿煜然。」
在旁,故為「上下弦也。」辰星體小,去日更近,難見其晦 明。因其運行不異,太白度亦與之同理。
問:「熒惑、歲星、填星孰遠近乎?」曰:「熒惑在歲、填星之內, 在日之外,何者?一為其行黃道,速於二星,遲於日也。 歲星在其次外,其行黃道速於填星,遲於熒惑也。填 星在於最外,其行黃道最遲也。又,恆星皆無視差,七 政皆有之,以此明其遠近。」又最確之證,無可疑者。
圖
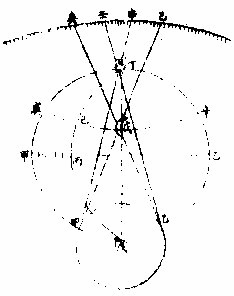
問何為視差曰如一人在極西一人在極東同一時仰觀七政則其躔度各不同也七政愈近人者差愈大愈遠者差愈小月最大日次之熒惑次之歲星又次之填星最小幾於無有故知月最近填星最遠也如上圖丙為地甲為東目
乙為「西目」,甲望戊月在己度,乙則在庚度,甲望丁星 在辛度,乙則在壬度。己庚差大,則月去人近,辛壬差 小,則星去人遠也。
問:「東西相去,既是極遠,何以得同在一時,仰觀七政?」 曰:「此在一時一地,亦可測之。特緣算數所得,難可遽 明,故以東西權說。若月食,則亦東西同時,兩地並測, 亦足證知也。」
問:「何以知七政之上,復有恆星之天?」曰:「恆星布列,終 古常然而一體東行,行度最遲,殆如不動。既與七政 異行,知其不得共居一天也。故當別有一恆星之天, 眾星皆麗其上矣。」
問:「恆星,天之上,何以知有宗動無星之天?」曰:「七政恆 星,其運行皆有兩種。其一自西而東,各有本行,如月 二十七日而周日,則一歲此類是也。其一自東而西, 一日一周者是也。非有二天,何能作此二動?故知七 政恆星之上,復有宗動一天,牽掣諸天,一日一周,而 諸天更在其中,各行其本行也。又七政恆星,既隨宗」 動西行,一日而周,其為「戚速」,殆非思議所及。而諸天 又欲各遂其本行,一東一西,勢相違悖。故近於《宗動》 東行極難;遠於《宗動》東行漸易。此又七政恆星遲速 所因矣。
問:「宗動天之上,又有常靜大天,何以知之?」曰:「今所論 者,度數也。姑以度數之理明之。凡測量動物,皆以一 不動之物為準。譬如舟行水中,遲速遠近若干道里, 何從知之?以離地知之,地本不動故也。若以此舟度 彼舟,何從可得?諸天自宗動以下,隨時展轉,八極不 同,二行各異。若以動論動,雜糅無紀,將何憑藉,用資」 考算。故當有不動之天,其上有不動之道。不動之極, 然後諸天運行,依此立算。凡所云某曜若干時,行天 若干度,分若干時,一周天之類,所言天者,皆此天也。 曆家謂之天元道。天元極、天元分,至此皆繫於靜天, 終古不動矣。
常靜篇第二
《總論》:〈凡一條:〉
《常靜天》者有三理:一為此下各動天之一切諸點。
七政恆星彗孛及諸道諸圈之交之分,但須測算者,總名為點。不言星者,交與分非星也。日月大矣,亦言「點。」 凡測皆測其心,心則點也。
藉此天以測知其所在也。二為測各動天運行之時 之度,與夫各點之出入隱見,以定歲月日時也。三為 測諸動天之各點,相去離幾何也。凡常靜天上諸名, 皆繫之天元,因其不動,以驗他動也。其最尊者有三 圈:一曰天元赤道圈。〈或稱中圈或稱腰圈下文通用〉以定諸點:二曰 「天元地平圈。」
或稱四方圈,或稱「八風」 圈,或稱「分光圈」 ,下文皆通用之。
以驗運行。三曰天元距圈。〈或稱去離圈下文通用〉以辨去離。
《論三圈》,〈凡七章。〉
論《天元赤道圈》,〈凡一條:〉
《天元赤道》者,繫於宗動之天,平分天體者也。
各圈各有心,天元赤道之心即「《大寰》之心」 也,即地心也。各圈各有極,各有軸,天元赤道之極之軸即「《大寰》之極之軸」 也,即「地之極之軸」 也。
《天元》赤道之左右各有距等圈。以度論,則九十為天。
圖
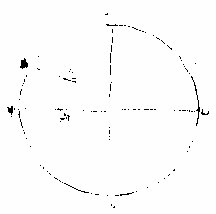
元緯圈其前後各有過極圈以度論則一百八十為天元經圈過極圈者所以定經度容緯度也
如上圖甲乙為中圈其上五經圈為甲丙有兩過極圈以限之丁甲戊限其首丁丙戊限其尾甲丙在其中是大圈上所容之六經
度也。又如丙己為過極圈上四緯圈則首尾兩點有兩距等圈以限之,甲丙乙限其首,庚己辛限其尾,丙 己在其中,是過極圈上所容之五緯度也。
論《天元地平圈》,〈凡三條:〉
常靜:「天下諸所測候,欲知各點所在與各點之道,各 道之交之分,則一中圈足矣。為地在中心,不能透明, 明為地隔。人在各所所見止有半天,其分明分暗處, 有一大圈,即地平圈也。地球之大,人居各所,明暗所 分,處處各異,故隨在有一地平圈。」
地平圈分為四象限,定天下之東西南北,故可曰方 道,亦可名風道,所謂「不周廣莫,八風所來」也。四象限 分為三百六十者,是地平之經度也。地平之兩端,一 在人頂為頂極,一在人對足之下為底極。地平之左 右各有距等小圈,從大圈至極各九十,為地平之緯 度。〈亦名高度亦名上度下文通用之〉其算以大圈為初度,次小圈為 一度,其最高為九十度,即頂極下亦如之。〈亦名低度亦名下度 下文通用之〉其最下為九十度,即底極也。從地平經度,每 度出一過頂,大圈凡一百八十,以定方維之分數。其
圖
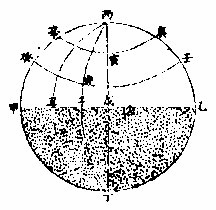
最尊而用大者有二一曰地平東西圈一曰地平南北圈如天元赤道上之有極至極分二圈也
極至極分見後篇
如上圖甲乙為地平丙為頂極丁為底極丙戊丁南北圈也甲丙乙丁東西圈也丙子丁丙丑丁皆經圈庚寅辛壬卯癸皆緯圈算
圖

地平之經度或從東西圈起或從南北圈起其緯度或從地平起或從頂極起各任用
地為圓體故球之上每一點各有一地平圈從人所居目所四望者即是其多無數
如右圖戊己為地,甲乙丙丁為天。人在戊即甲丙,是 其地平,而庚為頂極;人在己即乙丁,是其地平,而辛 為頂極。
《赤道地平二圈比論》,〈凡四條:〉
《常靜》天上有天元赤道,天元南北極恆定不動。就人 目所視,又有天元地平圈。今以二圈合論,則六合之 內共有三球:一為正球,二為欹球,三為平球。正有一 平,有一離,此即欹,欹者無數。
正球者,天元赤道之二極;在地平,則天元赤道與地
圖
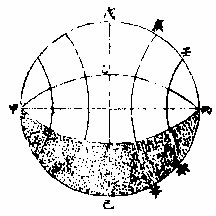
平為直角而其左右緯圈各半在地平上半在地平下
如上圖甲戊丙己圈為天甲乙丙丁線為地平甲丙即天元赤道之兩極戊乙丁己為地平之東西圈亦即天元赤道庚辛壬癸等則地平之經圈是正球也
《欹球》者,天元赤道之二極,一在地平上,一在地平下, 赤道與地平為斜角。〈斜角者一銳一鈍之總名〉而天元赤道與地 平之各經緯圈,伏見多寡各不等,其極出地之度,為 用甚大,測候者所必須也。赤道緯圈之中,隨地各有 一緯圈,為用甚大,名為「常見緯圈。」凡極出地若干度, 即有一去極若干度之緯圈,其底點常切地平者是 也。
如左圖,甲丙乙丁為地平,戊己為赤道極。若己乙為 極,出地四十度,則壬癸乙常見緯圈,亦去極四十度。
圖
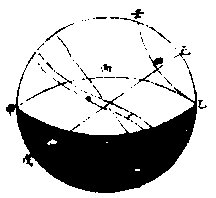
而緯圈之乙點即地平之乙點
平球者一極在頂天元赤道與地平為一線各距等圈皆與地平平行也如圖甲乙丙丁為地平即為天元赤道而戊極在頂庚辛等緯圈皆與地平平行
《論地平南北圈》,〈凡一條:〉
地平大圈上之過頂圈一百八十名頂圈,皆地平圈 之伴侶,故又名「侶圈。」其中大者二,曰東西,曰南北。其 又最尊者南北也。其兩極在地平與東西侶圈之交, 此圈平分球為東西二方,不但過頂極亦過天元赤 道極,與天元赤道相交為直角,亦不動與地平圈等。 但其游移也,人於地面上南北遷,此圈止有一,不得 「有二。東西遷則隨在不同與地平俱無數。」
如左圖,甲乙丙為南北圈,人在戊、在己、在庚俱南北
圖

一線則恆以甲乙丙圈為頂移極不移圈故云有一無二也若從己東西遷丁為其頂即以甲丁丙為南北圈矣
地平南北圈與天元赤道比論〈凡一條〉
此圈交於天元赤道即為天元赤道之極高從天元
圖

赤道至頂極之度即北極出地之度
如圖甲己為赤道丙為頂極乙為赤道極戊丁為地平今言甲丙與乙丁等者甲乙弧丙丁弧各相去九十度各減一丙乙弧則甲丙與乙丁等若赤道極高之甲戊弧亦與丙乙弧等
其理同也。
《論地平東西圈》,〈凡二條:〉
東西,亦地平之侶圈也。其兩極在地平與南北侶圈 之交,過此兩極者,有六大圈,亦分《天元球》為十二舍, 地平以上常見者六舍最尊者,地平與南北圈也。其 次序從東地平起算為初舍,入東一舍為第一,入東 二舍為第二,至南北圈之底起第四,西地平上起第 七,南北之頂起第十。此法為用甚大,醫家、農家及行 海者所必須也。
圖

如上圖丙丁壬為東西侶圈甲乙為兩極甲丁乙為地平圈甲戊乙甲庚乙等皆過極大圈也
其用之則以此圖甲乙丙丁為地平甲為東地平起一舍己為底極起四丙為西地平起七戊為頂極起十也
「東西圈平分球」為南北二方,造日晷必用之。
《論天元去離圈》,〈凡二條:〉
《天元》三大圈,其一赤道,其二地平。若欲知兩點相距 幾何,則二圈為未足也。故有去離大圈、過所設二點, 自此點至彼點其間之容則相去離之度分也。若此 二點俱在天元赤道,或俱在其過極圈,或俱在地平 圈,即所在圈為去離圈,不用《百游》去離圈。
《游者》游移不一,百言其多。
如左圖,甲乙丙丁線為地平,戊己為南北極,庚辛為
圖

黃道設壬癸點則子癸壬丑大圈上之癸壬是其度分
或問二點或俱在緯圈則即以緯圈為去離圈不可乎曰凡測量必用準分之尺度準度者止有一不得有二靜天上之大圈分則準度也各緯圈之小大與
其度分之廣狹,一一不等。若多寡不齊之尺度,豈能 得物之準分乎?故測去離,必用大圈,不得用緯圈也。 〈以上原本卷上。〉
Public domainPublic domainfalsefalse
![]()
本作品原文沒有標點。標點是人工智能程序古詩文斷句 v2.1創建,並且經由維基文庫用戶編輯改善的。本站用戶之編輯以知识共享 署名-相同方式共享 4.0协议(CC BY-SA 4.0)發佈。
歡迎各位持續修正標點,請勿複製與本站版權協議不兼容的標點創作。
![]()
Public domainPublic domainfalsefalse