钦定古今图书集成/历象汇编/历法典/第105卷

钦定古今图书集成
历象汇编 第一百五卷

钦定古今图书集成历象汇编历法典

　第一百五卷目录

　测量部汇考六

　　新法历书三〈测天约说上〉

历法典第一百五卷

测量部汇考六

《新法历书三》

测天约说上

“测天者，修历之首务；约说者，议历之初言也。不从测 候，无缘推算，故测量亟矣。即测候推算，亦非甚难不 可几及之事。所难者，其数曲而繁，其情密而隐耳。欲 御其繁曲，宜自简者始；欲穷其隐密，宜自显者始。”约 说之义，则总历家之大指，先为简显之说。大指既明， 即后来所作《易》言易知，渐次加详，如车向康庄，此为 发轫已。又古之造历者，不欲求明，抑将晦之，诸凡名 义，故为隐语。诸凡作法，多未及究论其所从来，与其 所以然之故，墙宇既峻，经途斯狭，后来学者，多不得 其门而入矣。此篇虽云率略，皆从根源起义，向后因 象立法，因法论义，亦复称之，务期人人可明，人人可 能，人人可改而止，是其与古昔异也。或云“诸天之说， 无从考证，以为疑义。”不知历家立此诸名，皆为度数 言之也。一切远近、内外、迟速、合离，皆测候所得，舍此 即推步之法，无从可用，非能妄作，安所置其疑信乎？ 若夫位置形模，实然实不然，则天载幽元，人灵浅鲜， 谁能定之？姑论而不议可矣。都为二卷，共八篇如左。

首篇

度数之学，凡有七种，共相连缀，初为二本：曰数，曰度。 数者，论物几何，众其用之，则算法也。度者，论物几何， 大其用之，则测法、量法也。

测法与“量法” 不异，但近小之物，寻尺可度者谓之“量法。” 远而山岳，又远而天象，非寻尺可度，以仪象测知之，谓之“测法。” 其量法如算家之专术，其测法如算家之缀术也。

“既有二本，因生三干：一曰视，人目所见，一曰听，人耳 所闻，一曰轻重，人手所揣。耳所闻者，因生乐器乐音。 手所揣者，因生举运之器。举运之法，惟目视一干，又 生二枝：一曰测天，一曰测地。”七者在西土庠士俱有 耑书。今翻译未广，仅有几何原本一种，或多未见未 习。然欲略举测天之理与法，而不言此理此法，即说 者无所措其辞，听者无所施其悟矣。七者之中，音乐 与轻重别为二家，故兹所陈，特举其四：曰“数”，曰“测量”， 曰“视”，曰“测地。”四学之中，又每举其一二，为卷中所必 需。其馀未及缕悉者，俟他日续成之也。为他篇所共 赖，故列于篇次之外，曰“首篇。”欲知他篇，须知此篇，故 又名《须知篇》。

数学一题

“比例”者，以两数相比，论其几何。

比例有二：一曰相等之比例，一曰不等之比例。若二 数相等，以此较彼无馀分，名曰“等比例”也。若二数不 等，又有二：一曰以大不等，一曰“以小不等。”如以四与 二相比，四之中凡为二者二，是为以大，即命曰“二倍 大”之比例也。如以二与四相比，倍其身乃得为四，是 为以小，即命曰“二分之一”之比例，或命曰“半比例”也。

测量学十八题

第一题至第十四题，《论测量之理》。

《第十五题至第十八题，论测量之法》：

几何原本书中，论线、论面、论体。今第一以至第五，论 线也。第六以至第十四，论体也。此书中不及面，故不 论面。

《几何原本》书中多言直线、圜线，其理易明，今不及论。 论其稍异者有五题，前二题言独线，后三题言两线。

第一题：〈独线一。〉

长圆形者，一线作圈，而首至尾之径大于腰间径，亦 名曰《瘦圈界》，亦名《撱圈》。

如甲乙丙丁圈形，甲丙与乙丁两径等，即成圈。今甲 首至丙尾之径，大于己至庚之腰间径，是名长圆。 或问此形何从生？答曰：“如一长圆柱，横断之，其断处。”

图

为两面皆圆形若断处稍斜其两面必稍长愈斜愈长或称卵形亦近似然卵两端小大不等非其类也

指其面曰平长圆若成体曰立长圆

第二题〈独线三〉

蛇蟠线者于平面上作一线自内至外恒平行恒为

图

圈线而不遇不尽如上图自甲至乙者是

旋风线者于平圆柱上作一线亦如蛇蟠但蜿蜒腾凌而上如旋风也

如上图自甲至乙者是螺旋线者于球上从腰至顶作一线如蛇蟠而渐高如旋风而渐小

如右图自“甲”至乙者是。

此书独用《螺旋线》，欲解其形势，故备言之。

第三题

下三题言《二线》者，或直，或不直。或相遇，或相离。

二线相遇者有三：但相遇而止，名曰“至线”；因至线在 所至线之上，故又曰“在上。”其割截而过者，名曰“交线”， 亦曰“割线”，亦曰“截线”；其至而不过又不止者，名曰“切 线”；其至线而有所分截者，亦称“割线”，或曰“截线”，或曰 “分线。”

图

如上图甲乙线与丙乙丁线丙乙丁圈相遇至乙而止则甲乙为至线又曰丙乙丁上线

如上三图甲乙线截丙丁线于戊己庚线截辛壬癸圈于辛子丑寅圈截丑卯寅圈于丑于寅皆谓之曰交线

图

又如上图甲乙线遇丙丁圈于丙戊己庚圈遇戊辛壬圈于戊皆名之曰切线也

如上图甲丙线分甲乙丙圈者曰分圈线亦曰割圈线亦曰截圈

第四题

两线不相遇而相离之度

图

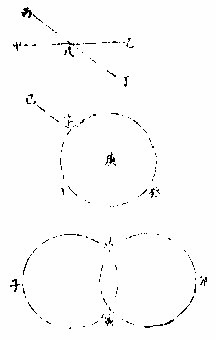
恒等名曰距等线

或称平行线侣线俱通用

如上三图甲至己乙至戊丙至丁其相离之度俱等

第五题

两线相遇即作角

本是一面为两线所限限以内即成角也

图

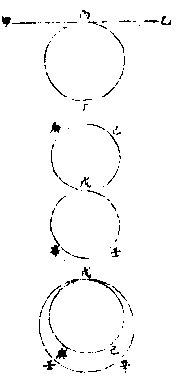
如上图甲乙与乙丙两线相遇于乙即包一甲乙丙角〈第二字即所指角〉其球上两圈线相交，亦作角。

如上图甲丙乙丁两线交而相分于戊即成甲成丁丁戊丙丙戊乙乙戊甲四球上角也

第六题

自此至第十四题皆论体。诸体中“球”为第一。此书所 用，独有球体，故未他及。

凡物之圆者，皆名“球。” 诸题中名义，凡立圆物皆有之，非独天也。

第《六至第八，言球内之理》；第《九至第十四，言球外之 理》。

球之内有心心者，从此引出线至球面，俱相等。 如左图：甲乙丙球，丁为心，从丁引出线至甲，至乙至

图

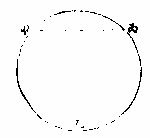
丙各等即作百千万线皆等

第七题〈球内〉

径者一直线过球心两端各至面半径者从心至面如上图甲乙球丙为心一直线过丙两端至甲至乙即甲乙为径线其丙乙丙甲皆为半径线

图

第八题〈球内〉

球不离于本所而能旋转则其一径之不动者名为轴轴之两端名为两极也凡一球止有一心凡球之转止有一轴其径甚多无数可尽

如上图甲乙丙丁球戊为心乙丁过心此球从甲向

丙丙又向甲旋转而不离其处，则乙戊丁直线为不

动之处，是名轴也。乙与丁则为两极球心，若离于戊 点如己，则从心所出两半径线如庚己，己辛必不等， 故曰“止有此心。”凡轴皆利转，若有二轴，二俱转即相 碍，一不转即非轴，故曰“止有一轴。从心出直线。”苟至 面皆径也，故曰“无数。”

《第九题》：〈球外：〉

球之面可作多圈，圈有大有小，大圈者，其心即球心， 若从圈剖球为二，则其圈之径过球心也。各大圈从

图

圈面作垂线各有其本圈之轴与其两极

如上图甲乙丙丁球上作甲戊丙己大圈其垂线乙丁即乙丁为本圈之轴乙丁两点即其两极故大圈在两极之间离两极俱相等

第十题〈球外〉

图

小圈者不分球为两平分不与球同心其去两极一近一远愈近所向极愈小愈近心愈大

如上图甲乙为大圈丙丁戊己庚皆小圈也故一大圈之上之下可作无数小圈众小圈之间止可作一大圈

第十一题：〈球外：〉

圈不论大小，其分之有三等。

“三等”者，一曰大分，一曰小分，一曰细分。如两平分之 为半圈，四平分之为象限，此大分也。每象限分为九 十度，此小分也。每度又析为百分，每分为百秒，递析 为百至纤而止。《西历》则每度析为六十分，每分为六 十秒，递析为六十至十位而止，此细分也。

第十二题：〈球外：〉

两大圈交而相分为角。欲测其角之大从交数两弧。

图

各九十度而遇过极之圈两弧所容过极圈之弧度分即命为本角之度分如上图戊丁乙为过极圈有甲乙丙甲丁丙两大圈交而相分于甲于丙问丁甲乙角为几何度分之角法从甲交数各九十度而遇过极之戊丁乙圈为甲

丁甲乙此两弧间所容过极圈之分，为丁乙弧。如丁 乙六十度，即命丁甲乙角为六十度角。

《第十三题》：〈球外：〉

凡大圈俱相等，两大圈交而相分，其所分之圈分两 俱相等。

凡大圈必于本球之腰。腰者，最大之线也。凡最大之 线止有一，不得有二，故展转作无数大圈，俱相等。圈 既相等，则以大圈分大圈，其两交线必在球之腰，此 交至彼交，必居球之半，故无数大圈各相分所分之。

图

两圈分各相等有不等者即小圈也

第十四题〈球外〉

大圈俱相等故所分之度分秒各所容皆相等小圈各不相等故度分秒之名数等其所容各不等如上图甲乙己为大圈丙丁戊为小圈大圈既相等

即多作大圈，皆与甲、乙、己圈等，而各圈之甲至乙其 度皆等。若丙、丁、戊小圈既与甲、乙、己大圈不等，则甲 至乙与丙至丁同名为若干度，而所容之广狭不等。

第十五题：〈以下四题，言测量之法。〉

长方面，其中任设一点，欲定其所在为何度分，作经 纬度求之。

法曰：先平分其长为若干度分，名经线。次平分其广 为若干度分，名“纬线。”经与纬每度分之小大俱等。次 视经纬之线，其过点各若干度分，即命为点所在之。

图

度分

如上图甲乙丙丁长方形欲知戊点所在先从乙向丙作距等经线次从乙向甲作距等纬线次视戊点在经纬线之交为是何度即命曰在经度之四纬度之八也

乙至丙丙点得命为第

六、乙点，不得命为第一，而命为初，历家言“算外” 者俱准此。

第十六题

其在球也亦如之。球之中任设一点，欲定其所在为 何度分，亦先作球之经度。

法曰：先于两极之间作一大圈，为腰圈，平分腰圈为 三百六十度，从各度各作一过极大圈，即半圈平分 为一百八十度，是为腰圈上之经度。

如左图甲乙丙丁球乙丁为两极，于其间，作甲戊丙。

图

己腰圈从戊向丙丙向己各作过极大圈即乙庚丁乙辛丁等线皆腰圈上之经度

第十七题

次作球之纬度即定所设点在何度分

腰圈之两旁有两极从腰圈向极分为九十度每度

图

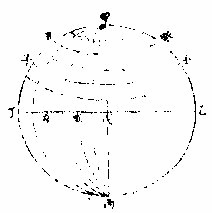
各作一距等小圈渐远腰渐小至极而为一点即第九十小圈也次视经纬两线之交命在设点在何度分

如图甲乙丙丁球上依前题既作甲庚丙甲辛丙各经线次于乙戊丁腰圈上向甲极分为九十度每度

各作一距等小圈，如壬子、癸丑之类，皆纬圈也。次视 经纬各遇点之交，从腰圈线考其经度，从过极线考 其纬度，即命所设己点在从戊向丁之第四经圈，从 戊向甲之第三纬圈。

凡言“度”者，各有二义。其一，一度之广能包一度之地， 是其容也。其一，自此度至彼度，各以一点为界，是其 限也。《腰圈度》之容，以各过极度之线限之，过极度之 容，以各距等线限之。

凡圈互相为经，亦互相为纬。如以过极为经，则距等 为纬，若以距等为经，则过极为纬。如几何原本之论， 线互相为直线互相为垂线也。

第十八题

《论纬圈以大圈为宗》，

过极经圈，皆大圈也，皆等距等线限之。诸度分之容， 亦等距等纬圈，皆小圈也，各不等。过极圈限之诸度 分之容，愈近极愈狭，至极而尽矣。故纬度之容，等于 经度者，独有腰圈一线，独有初度初分初秒之一率。 过此以上，无不狭也，故当以大圈为宗。大圈左右诸

图

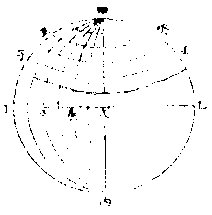
纬圈之上凡言经度之容者皆从此推减之圈愈小度愈狭即差愈多也

视学一题

凡物必有影影有等有大小有尽有不尽

不透光之物体前对光体后必有影焉若光体大于物体其影渐远渐杀锐极

而尽。若光体小于物体，其影渐远渐大，以至无穷。若 光物相等。其影亦相等亦无穷。

测地学四题

第一题

“地为圆体”，与海合为一球。

何以征之？凡人任于一处向北行二日半，则北方之 星在子午线上者必高一度；次后二日半复高一度。 恒如是为相等之差。向南行亦如之。知从南至北为 圆体也。

图

如上图甲为北星丁为南星乙辛丙圈为地球人在乙则见甲正在其顶至戊则少一度矣从戊至己与乙至戊道里等又少一度矣迨至辛则不见甲至壬则反见丁安得非圆体乎若云地为平体则见星当如癸从丑向寅至辰宜常

“见不隐。”又丑至寅，寅至卯，若见子之高下所差等，则 道里宜不等。〈别有筭数〉“安得有时不见。”又恒为相等之差 也。

若人东行渐远，则诸星出地者渐先见，西行渐远渐 后见。故东西人见，日月食迟速先后各异，是知东西 必圆体也。

第二题

地在《大圜》，天之最中，

何以征之？人任于所在见天星，半恒在上，半恒在下

图

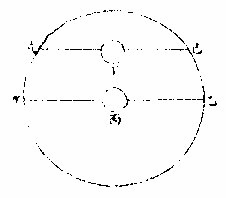
故知地在最中也

如上图丙为地东见甲西见乙甲乙以上恒为天星之半知丙在中也若云非中当在丁则东望戊西望己当见天之小半而不见者大半

第三题

地之体恒不动

一、不去本所；二、亦不旋转。云“不去本所”者，去即不在， 天之最中也。云在本所，又不旋转者，若旋转，人当觉 之，且不转则已，转须一日一周，其行至速。一切云行 鸟飞，顺行则迟，逆行则速。人或从地掷物空中，复归 于地，不宜在其初所。今皆不然，足明地之不转。

第四题

地球在天中止于一点，

何以征之？人在地面，不论所在，仰视填星、岁星、荧惑， 彼此所见，恒是同度，故知地体较于天体，则为极小。

图

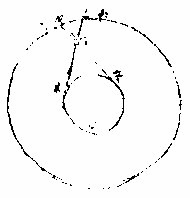
若地大者两人相去绝远其视三星彼此所见不宜同躔

如上图丙己戊乙为天甲为地丁为星地体若大能为天分数者则人在庚宜见丁在己度人在辛宜见丁在戊度今不然者是地与天其小大无分数可论

也。

名义篇第一

《测天本义》，〈凡一条：〉

问：“测天者何事，所论者何义也？”曰：“此度数之学。度数 学有七支，此为第六也。所论者一言三曜。”〈日月星〉形象 大小之比例，一言其各去离地心地面各几何，一言 其运动自相去离几何，一言其躔离逆顺、晦明朓朒， 一言其五相视。五相视者，一曰“会聚。”

《会聚》或同一宿，或同一宫，或相掩，或凌犯。

二曰《六合照》。〈每隔一宫〉三曰“隅照。”〈三方相望〉四曰“方照。”〈四方相望〉五 曰“对照。”〈即冲〉一、因其行度次舍，以定岁月日时，此为大 端也。

《大圜》名数：〈凡十条：〉

《大圜》者，上天下地之总名也。

亦称“宇宙” ，亦称“天下” ，亦称六合之内，下文通用。

天实浑圆，其中毫无空隙。譬如葱本，重重包裹，其分 数几何，则自下数之。〈地居天中为最下亦曰最内〉第一为地水补 其阙。

“地有庳洼，水则就之，若据地面，则水土相半。” 跖实论之，水之视地，仅当千分之一。

共为一球。地外为气，气之外为“《七政》之天”，七政之外 为恒星。〈亦曰经星下文通用〉“之天”，“恒星之外，为宗动之天”，“宗动 之外，为常静之天。”

问：“地水与气，相次之序，其理解易明。今何以知七政 在下，恒星在上？”曰：“有二验焉：其一，六曜有时能掩恒 星。”

六曜者，月五星也。不言“日” 者，日大光星不可见也。唐肃宗上元元年五月癸丑，月掩昴。代宗大历三年正月壬子，月掩毕；八月己未，月复掩毕。是月掩恒星也。唐高宗永徽三年正月丁亥，岁星掩太微上将；五月戊子，荧惑掩右执法。元武宗至大元年十二月戊寅，太白掩建星。是五纬掩恒星也。

“掩之”者在下，所掩者在上也。其二七政循黄道，行皆 速，恒星最迟也。

问：“七政中复有上下远近否？”曰：“有之，月最近也。何以 知之？亦有二验：其一能掩日五星也。”

月掩日而日为食，不待论也。唐文宗太和五年二月甲申，月掩荧惑。六年四月辛未，月掩填星于端门。九年六月庚寅，月掩岁星于太微。武宗会昌二年正月壬戌，月掩太白于羽林，是月掩五星也。

其二，循黄道行二十七日有奇而周天，馀皆一年以 上，是七政中为最速也。

问“行度迟速，以别远近，是则然矣。太白辰星与日同 一岁而周，为无远近乎？”曰：“旧说或云日内月外，相去 辽绝，不应空然无物，则当在日天之下；或云在日天 之上。二说皆疑，了无确据。若以相掩正之，则大光中 无复可见。论其行度，则三曜运旋，终古若一。两术既 穷，故知从前所论，皆为臆说也。独西方之国，近岁有” 度数名家，造为望远之镜，以测太白，则有时晦，有时 光满，有时为上下弦计。太白附日而行，远时仅得象 限之半，与月异理，因悟时在日上，故光满而体微。

若地日星参直，则不可见，稍远而犹在上，则若几望之月也。

《时在日下》则晦

《三》、“参直故晦，稍远而犹在下若复苏之月，体微而光燿煜然。”

在旁，故为“上下弦也。”辰星体小，去日更近，难见其晦 明。因其运行不异，太白度亦与之同理。

问：“荧惑、岁星、填星孰远近乎？”曰：“荧惑在岁、填星之内， 在日之外，何者？一为其行黄道，速于二星，迟于日也。 岁星在其次外，其行黄道速于填星，迟于荧惑也。填 星在于最外，其行黄道最迟也。又，恒星皆无视差，七 政皆有之，以此明其远近。”又最确之证，无可疑者。

图

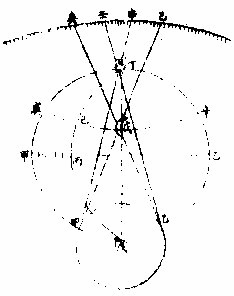
问何为视差曰如一人在极西一人在极东同一时仰观七政则其躔度各不同也七政愈近人者差愈大愈远者差愈小月最大日次之荧惑次之岁星又次之填星最小几于无有故知月最近填星最远也如上图丙为地甲为东目

乙为“西目”，甲望戊月在己度，乙则在庚度，甲望丁星 在辛度，乙则在壬度。己庚差大，则月去人近，辛壬差 小，则星去人远也。

问：“东西相去，既是极远，何以得同在一时，仰观七政？” 曰：“此在一时一地，亦可测之。特缘算数所得，难可遽 明，故以东西权说。若月食，则亦东西同时，两地并测， 亦足证知也。”

问：“何以知七政之上，复有恒星之天？”曰：“恒星布列，终 古常然而一体东行，行度最迟，殆如不动。既与七政 异行，知其不得共居一天也。故当别有一恒星之天， 众星皆丽其上矣。”

问：“恒星，天之上，何以知有宗动无星之天？”曰：“七政恒 星，其运行皆有两种。其一自西而东，各有本行，如月 二十七日而周日，则一岁此类是也。其一自东而西， 一日一周者是也。非有二天，何能作此二动？故知七 政恒星之上，复有宗动一天，牵掣诸天，一日一周，而 诸天更在其中，各行其本行也。又七政恒星，既随宗” 动西行，一日而周，其为“戚速”，殆非思议所及。而诸天 又欲各遂其本行，一东一西，势相违悖。故近于《宗动》 东行极难；远于《宗动》东行渐易。此又七政恒星迟速 所因矣。

问：“宗动天之上，又有常静大天，何以知之？”曰：“今所论 者，度数也。姑以度数之理明之。凡测量动物，皆以一 不动之物为准。譬如舟行水中，迟速远近若干道里， 何从知之？以离地知之，地本不动故也。若以此舟度 彼舟，何从可得？诸天自宗动以下，随时展转，八极不 同，二行各异。若以动论动，杂糅无纪，将何凭借，用资” 考算。故当有不动之天，其上有不动之道。不动之极， 然后诸天运行，依此立算。凡所云某曜若干时，行天 若干度，分若干时，一周天之类，所言天者，皆此天也。 历家谓之天元道。天元极、天元分，至此皆系于静天， 终古不动矣。

常静篇第二

《总论》：〈凡一条：〉

《常静天》者有三理：一为此下各动天之一切诸点。

七政恒星彗孛及诸道诸圈之交之分，但须测算者，总名为点。不言星者，交与分非星也。日月大矣，亦言“点。” 凡测皆测其心，心则点也。

借此天以测知其所在也。二为测各动天运行之时 之度，与夫各点之出入隐见，以定岁月日时也。三为 测诸动天之各点，相去离几何也。凡常静天上诸名， 皆系之天元，因其不动，以验他动也。其最尊者有三 圈：一曰天元赤道圈。〈或称中圈或称腰圈下文通用〉以定诸点：二曰 “天元地平圈。”

或称四方圈，或称“八风” 圈，或称“分光圈” ，下文皆通用之。

以验运行。三曰天元距圈。〈或称去离圈下文通用〉以辨去离。

《论三圈》，〈凡七章。〉

论《天元赤道圈》，〈凡一条：〉

《天元赤道》者，系于宗动之天，平分天体者也。

各圈各有心，天元赤道之心即“《大寰》之心” 也，即地心也。各圈各有极，各有轴，天元赤道之极之轴即“《大寰》之极之轴” 也，即“地之极之轴” 也。

《天元》赤道之左右各有距等圈。以度论，则九十为天。

图

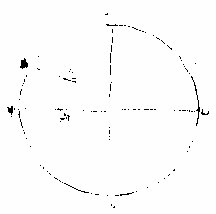
元纬圈其前后各有过极圈以度论则一百八十为天元经圈过极圈者所以定经度容纬度也

如上图甲乙为中圈其上五经圈为甲丙有两过极圈以限之丁甲戊限其首丁丙戊限其尾甲丙在其中是大圈上所容之六经

度也。又如丙己为过极圈上四纬圈则首尾两点有

两距等圈以限之，甲丙乙限其首，庚己辛限其尾，丙 己在其中，是过极圈上所容之五纬度也。

论《天元地平圈》，〈凡三条：〉

常静：“天下诸所测候，欲知各点所在与各点之道，各 道之交之分，则一中圈足矣。为地在中心，不能透明， 明为地隔。人在各所所见止有半天，其分明分暗处， 有一大圈，即地平圈也。地球之大，人居各所，明暗所 分，处处各异，故随在有一地平圈。”

地平圈分为四象限，定天下之东西南北，故可曰方 道，亦可名风道，所谓“不周广莫，八风所来”也。四象限 分为三百六十者，是地平之经度也。地平之两端，一 在人顶为顶极，一在人对足之下为底极。地平之左 右各有距等小圈，从大圈至极各九十，为地平之纬 度。〈亦名高度亦名上度下文通用之〉其算以大圈为初度，次小圈为 一度，其最高为九十度，即顶极下亦如之。〈亦名低度亦名下度 下文通用之〉其最下为九十度，即底极也。从地平经度，每 度出一过顶，大圈凡一百八十，以定方维之分数。其

图

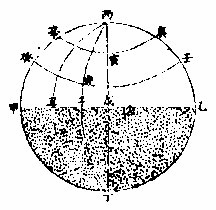
最尊而用大者有二一曰地平东西圈一曰地平南北圈如天元赤道上之有极至极分二圈也

极至极分见后篇

如上图甲乙为地平丙为顶极丁为底极丙戊丁南北圈也甲丙乙丁东西圈也丙子丁丙丑丁皆经圈庚寅辛壬卯癸皆纬圈算

图

地平之经度或从东西圈起或从南北圈起其纬度或从地平起或从顶极起各任用

地为圆体故球之上每一点各有一地平圈从人所居目所四望者即是其多无数

如右图戊己为地，甲乙丙丁为天。人在戊即甲丙，是 其地平，而庚为顶极；人在己即乙丁，是其地平，而辛 为顶极。

《赤道地平二圈比论》，〈凡四条：〉

《常静》天上有天元赤道，天元南北极恒定不动。就人 目所视，又有天元地平圈。今以二圈合论，则六合之 内共有三球：一为正球，二为欹球，三为平球。正有一 平，有一离，此即欹，欹者无数。

正球者，天元赤道之二极；在地平，则天元赤道与地

图

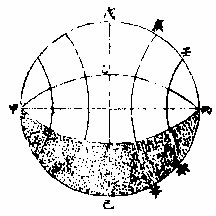
平为直角而其左右纬圈各半在地平上半在地平下

如上图甲戊丙己圈为天甲乙丙丁线为地平甲丙即天元赤道之两极戊乙丁己为地平之东西圈亦即天元赤道庚辛壬癸等则地平之经圈是正球也

《欹球》者，天元赤道之二极，一在地平上，一在地平下， 赤道与地平为斜角。〈斜角者一锐一钝之总名〉而天元赤道与地 平之各经纬圈，伏见多寡各不等，其极出地之度，为 用甚大，测候者所必须也。赤道纬圈之中，随地各有 一纬圈，为用甚大，名为“常见纬圈。”凡极出地若干度， 即有一去极若干度之纬圈，其底点常切地平者是 也。

如左图，甲丙乙丁为地平，戊己为赤道极。若己乙为 极，出地四十度，则壬癸乙常见纬圈，亦去极四十度。

图

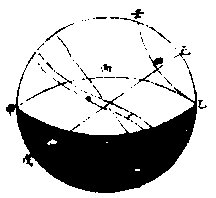
而纬圈之乙点即地平之乙点

平球者一极在顶天元赤道与地平为一线各距等圈皆与地平平行也如图甲乙丙丁为地平即为天元赤道而戊极在顶庚辛等纬圈皆与地平平行

《论地平南北圈》，〈凡一条：〉

地平大圈上之过顶圈一百八十名顶圈，皆地平圈 之伴侣，故又名“侣圈。”其中大者二，曰东西，曰南北。其 又最尊者南北也。其两极在地平与东西侣圈之交， 此圈平分球为东西二方，不但过顶极亦过天元赤 道极，与天元赤道相交为直角，亦不动与地平圈等。 但其游移也，人于地面上南北迁，此圈止有一，不得 “有二。东西迁则随在不同与地平俱无数。”

如左图，甲乙丙为南北圈，人在戊、在己、在庚俱南北

图

一线则恒以甲乙丙圈为顶移极不移圈故云有一无二也若从己东西迁丁为其顶即以甲丁丙为南北圈矣

地平南北圈与天元赤道比论〈凡一条〉

此圈交于天元赤道即为天元赤道之极高从天元

图

赤道至顶极之度即北极出地之度

如图甲己为赤道丙为顶极乙为赤道极戊丁为地平今言甲丙与乙丁等者甲乙弧丙丁弧各相去九十度各减一丙乙弧则甲丙与乙丁等若赤道极高之甲戊弧亦与丙乙弧等

其理同也。

《论地平东西圈》，〈凡二条：〉

东西，亦地平之侣圈也。其两极在地平与南北侣圈 之交，过此两极者，有六大圈，亦分《天元球》为十二舍， 地平以上常见者六舍最尊者，地平与南北圈也。其 次序从东地平起算为初舍，入东一舍为第一，入东 二舍为第二，至南北圈之底起第四，西地平上起第 七，南北之顶起第十。此法为用甚大，医家、农家及行 海者所必须也。

图

如上图丙丁壬为东西侣圈甲乙为两极甲丁乙为地平圈甲戊乙甲庚乙等皆过极大圈也

其用之则以此图甲乙丙丁为地平甲为东地平起一舍己为底极起四丙为西地平起七戊为顶极起十也

“东西圈平分球”为南北二方，造日晷必用之。

《论天元去离圈》，〈凡二条：〉

《天元》三大圈，其一赤道，其二地平。若欲知两点相距 几何，则二圈为未足也。故有去离大圈、过所设二点， 自此点至彼点其间之容则相去离之度分也。若此 二点俱在天元赤道，或俱在其过极圈，或俱在地平 圈，即所在圈为去离圈，不用《百游》去离圈。

《游者》游移不一，百言其多。

如左图，甲乙丙丁线为地平，戊己为南北极，庚辛为

图

黄道设壬癸点则子癸壬丑大圈上之癸壬是其度分

或问二点或俱在纬圈则即以纬圈为去离圈不可乎曰凡测量必用准分之尺度准度者止有一不得有二静天上之大圈分则准度也各纬圈之小大与

其度分之广狭，一一不等。若多寡不齐之尺度，岂能 得物之准分乎？故测去离，必用大圈，不得用纬圈也。 〈以上原本卷上。〉