欽定古今圖書集成/經濟彙編/樂律典/第059卷

欽定古今圖書集成
經濟彙編 第五十九卷

欽定古今圖書集成經濟彙編樂律典

　第五十九卷目錄

　律呂部彙考十三

　　明唐荊川稗編〈求元聲法　制管之法　十二宮去其中管為七　頭管即古

　　管〉

　　韓苑洛志樂一〈律呂說　律呂直解　黃鐘分寸圖　黃鐘管圖　林鐘管圖

　　　大蔟管圖　南呂管圖　姑洗管圖　應鐘管圖　蕤賓管圖　大呂管圖　夷則管圖

　　夾鐘管圖　無射管圖　仲呂管圖〉

樂律典第五十九卷

律呂部彙考十三

《明唐荊州稗編》

求元聲法

《律書》曰：「黃鐘之實，十七萬七千一百四十七，管長九 寸。」是十二律之管，惟黃鐘之宮為最長，故謂之元聲， 猶言頭一聲也。然所謂九寸者，非度之以凡尺，本乎 人聲而得之也。其法：令歌者作聲，取其最下一聲，而 以竹長九寸、上下空、圍九方分者為管，吹其體中翕 聲以效之。視管聲比人聲稍高，則增管令長，比人聲 稍下，則減管令短，上下游移以裁之，必其與人聲合 一而無差，乃以此管命為九寸黃鐘之宮也。次以子 穀秬黍中者一千二百粒實管中，視黍不足則易管 令小，有餘則易管令大，以此管命為黃鐘徑圍，是謂 以聲生律，以律生尺，而元聲在是矣。此管體中翕聲 謂之「合」字，以「合」字寫之，琴瑟第一絃鐘磬第一板，箎 笛第一孔，笙竽第一簧，則八音皆正。以此管上下相 生，即得已後十一律，而律呂皆正。宋儒程顥曰：「清者 極吹盡清，濁者極吹盡濁，嚮中間折取一聲，即口中 聲。」蓋以黃鐘之半律為中聲也。其法與此同。

制管之法

「元不師古，無足道者。惟太史院景表尺乃郭守敬所 造，守敬精於律曆，決非苟作，今欽天監表尺是也，比 市尺只得八寸強。」愚嘗取黑黍，揀其中者一千二百 粒，日乾之，稱重五錢者，以九十粒橫累之，命為九寸， 與表尺合。又截竹為管，長同黍寸，其竅上下均容一 千二百黍者，吹之，其聲與人之最下一聲合，是為黃 「鐘之聲」，制管之法，可謂簡易而無難矣。

黃鐘宮俗呼「正宮」，　　　商俗呼《大石調》。

角，俗呼《大石角調》。　　　羽，俗呼《般涉調》。

大呂宮俗呼《高宮》　　　商俗呼《高大石調》；

角俗呼《高大石》《角。　　　羽》俗呼《高般涉》。

太簇宮，俗呼中管《高宮　；商》，俗呼中管《高大石 角》，俗呼中管《高大石角　；羽》，俗呼「中管《高般涉》。」 夾鐘宮，俗呼「中呂宮」　　；《啇》，俗呼「雙調 角」，俗呼「雙調」《角　　　　羽》，俗呼「中呂調。」

姑洗宮，俗呼中管中呂宮。」　《啇》，俗呼「《雙調； 角》、俗呼「中管《雙角調》」　　　；《羽》，俗呼「中呂調。」

仲呂宮俗呼《道調宮》。　　　商俗呼《小石調》。

角，俗呼「小石角調。」　　　　羽，俗呼「正平調。」

蕤賓宮，俗呼中管《道調宮　商》」，俗呼「中管《小石調。 角》，俗呼「中管《小石角調》」　　；《羽》，俗呼「中管《正平調》。」 林鐘宮，俗呼「南呂《宮　　　商》」，俗呼「歇指調。」

角、俗呼「歇指《角調》。」　　　　羽，俗呼「高平調。」

《夷則宮》，俗呼「仙呂宮。」　　　商俗呼「商調。」

角，俗呼「商角調。」　　　　　羽，俗呼「仙呂調。」

《南呂宮》，俗呼中管《仙呂宮。　商》，俗呼中管《商調 角》，俗呼《中管商》。《角調　　　羽》，俗呼「中管《仙呂調》。」 《無射宮》，俗呼《黃鐘宮。　　　商》，俗呼「越調。」

《角》，俗呼《越角調》。　　　　　《羽》，俗呼《羽調》。

應鐘宮，俗呼「中管《黃鐘宮》」　；《商》，俗呼「中管《越調》。」 《角》，俗呼「中管《越角調》。」　　　《羽》，俗呼「中管《羽調》。」

十二宮去其中管為七

臣按：十二宮用七，去其中管而言也。自子黃鐘至亥 應鐘，十二宮各具七聲，共八十四聲，內寅太簇七聲， 與丑大呂七聲同，字譜宮聲同四字、商聲同一字、角 聲同上勾徵、聲同工字、羽聲同凡字。辰姑洗七聲，與 卯夾鐘七聲同，字譜宮聲同一字、商聲同上勾徵、聲 同「凡」字，惟角羽二聲有尺、工、六五之異。酉南呂七聲， 與申夷則七聲同。《字譜》宮聲同工字，商聲同凡字，徵 聲同一字，羽聲同上勾，惟角聲有六五之異。午蕤賓、 亥應鐘，亦各七聲，雖與前位不同，然黃鐘均內，以蕤 賓為變徵，應鐘為變宮，二變名曰「和」，謬不可為調。已 上五宮共五七三十五調，皆以中管名之。中管雲者， 謂其聲在前後二律之間，而與前律同出一孔，以之 製調，音韻重。雖強易其名，終無所表異。視前律為不 逮，故不用也。十二宮除此外七宮而已。唐祖孝孫參 定《雅樂》，古鐘十二，近代惟用其七，餘五鐘仍號「啞鐘」， 莫能通者。張文收吹律調之五鐘，皆響徹。蓋鐘無不 響者，以不用故以「啞」名之。隨管擊之，寧得不應？當時 蓋未考中管之說耳。

===頭管即古管===

頭管九孔，自下而上，管體中翕然為「合」字，第一孔「四」

字，第二孔「一」字，第三孔「生」字，第四孔後出「勾」字，第五 孔「尺」字，第六孔「工」字，第七孔「凡」字，第八孔後出「六」字， 第九孔「五」字。大樂以此先諸樂，謂之頭管。《經》曰「嘒嘒 管聲，下管象武」之類是也。

管色字譜五，凡工尺上四六一勾，合管九孔六勾二 字，並後出「合」字，在管體中。自下而上「合」字為黃鐘正 聲下四，大呂高四，太簇共第一孔下一，夾鐘高一，姑 洗共第二孔上字，仲呂第三孔「勾」字，蕤賓後出第四 孔「尺」字，林鐘第五孔下工，夷則高工，南呂共第六孔 下凡，無射高凡，應鐘共第七孔六字，黃鐘清後出第 八孔，下五大呂清，高五太簇清，緊五夾鐘清，共第九 孔，九孔，內四一工。凡皆有高、下二聲五字。有高、下、緊 三聲，惟上勾、尺無高下。蓋仲、蕤林三律，不分清濁，自 然應律也。十字者，載籍無可考，惟《楚辭·大招》曰：「二八 接武，投詩賦只。叩鐘調磬，娛人亂只。」「四上競氣，極聲 變只。」註曰：「四上未詳。」今按《招魂》曰：「吳歈蔡謳，奏大呂 些。」大呂為宮，其譜下四；仲呂為角，其譜上字，四上競 氣，謂宮、角相應也。

《韓苑洛志樂一》

律呂說

陳氏《樂書》曰：「甚哉！諸儒之論律呂，何其紛紛邪？謂陰 陽相生自黃鐘始，而左旋八八為伍，管以九寸為法 者，班固之說也。生倍實，上生四實，皆三其法，而管又 不專以九寸為法者，司馬遷之說也。持隔九相生之 說，以中呂上生黃鐘，不滿九寸，謂之執始，下生去滅， 上下相生，終於《南事》，十二律之外，更增六八，為六十 律」者，京房之說也。本《呂覽》、淮南王安、蔡邕之說，建蕤 賓重上生之議。至於大呂、夾鐘、仲呂之律，所生分等， 又皆倍焉者，鄭康成之說也。隔七為上生，隔八為下 生，至於仲呂則孤而不偶，蕤賓則踰次無準者，劉向 之說也。演京房南事之餘而伸之為三百六十律，日 當一管，各以次生者，宋錢樂之之說也。斥京房之說， 而以新舊法分度參錄之者，何承天、沈約之說也。「校 定黃鐘，每律減三分，而以七寸為法」者，隋劉焯之論 也。析毫釐之彊弱為筭者，梁武帝之法也。由此觀之， 諸儒之論，角立蜂起，要之最為精密者，班固之志而 已。今夫陰陽之聲，上生者三分之外益一，下生者三 分之內損一。蓋古人簡易之法，猶古歷周天三百六 十五度四分度之一也。若夫律同之聲，適多寡之數， 長短之度，小大之量，清濁之音，一要宿乎中聲而止， 則動黃鐘而林鐘應，動無射而仲呂應，和樂未有不 興者矣。黃鐘距地面有淺深，必也洛陽乎天地之中， 陰陽之會也，然後淺深之應的。

律不求元聲，元氣雖能宰物，終是苟且，與天地何與？ 然聖人得元聲以候元氣，今當候元氣以求元聲，律 能應氣，度量、衡由之而定。凡八音之輕重、厚薄、大小、 多寡、長短由於律，其體則天地之體，宜其用之能感 天地也。

「聖人不能以一身周天下之用，故制為器數，以教萬 世。」是以天下後世，人非聖人，而道則聖人之道也。昔 孔子聞《韶》於齊，夫其考擊而搏拊者，固非皆夔倫也， 而其美如此者，器數存也。且聖人之道，有文有本，天 地之道，有纖有洪，自然之理也。今不論度量衡之數， 而曰妙在其人，則聖人當時止為一支之木，一塊之 土，一鉤之金足矣，何必為鐘為鼓，為笙為磬？又從而 為篁為絃，有煩有簡若是哉？今試以祭祀之時，燕享 之際，琴瑟缺其絃，笙盡去其篁，鑄萬鈞為鎛鐘，合以 方寸之鞀鼓又從而盡去八音，使寶常擊食器，荀勖 搖牛鐸，可乎不可乎？是故君子不為無益之空言，必 究製作之實用。

「自隋、唐以來，律皆造作，用金刀剖削而成，非本然之 管，恐傷元氣。且律呂絲忽所爭，若非良工剖削之際， 安能適中？」予謂多取竹管，其從長未免用刀斷之，必 求徑三分四釐六毫、周廣十分三釐六毫者而後用 之，庶得聲氣之元矣。律雖非生於累黍，然古樂既亡 律管，非累黍亦何由定？予謂亦須自九十黍累為九 「寸，然後依蔡氏之說，多截竹管，或長一分，或半分，或 十分分之一，以至於九；或短一分，或半分，或十分分 之一，以至於九，中間必有適之者矣。」

埋管之地，不可以城市之中。蓋城市之地，翻取數過， 皆灰糞瓦礫，非本然之土，必於曠野素無人居之地。 土之黃壤者，亦須去二三尺以盡客土，撅亦不可深， 深則恐傷正氣。如此候之，或得正氣之應矣。

器與造化通，唯律而已。黃鐘既定，凡天地之器，雖衣 服盤盂，皆造化之運。形而上，形而下，本一物也。《明律 義》，凡天下之理皆可通，不但為作樂而已，太極之理， 亦不外此也。

「八音之數，惟絲為自然」，其七音皆倚此而起數，絲忽 之際，其微矣乎？

「春陽無不到，陵原無二氣《蕤賓》隔八。」若益一分，上生大呂，與損一分下生大呂， 倍其數，長短不差絲毫。然不如下生為自然，於十二 律之序為順。審思自見。

「大呂」當為十月管，逆數至應鐘為《夏至》。

今尺惟車工之尺最准，萬家不差毫釐，少不似則不 利載，是孰使之然哉？古今相沿，自然之度也。然今之 尺，則古之尺二寸也，所謂尺二之軌，天下皆同是也。 以木工尺去二寸，則周尺也。昔魯公欲高大其宮室， 而畏王制，乃以時尺增一寸，召班授之。班知其意，後 增一寸，進於公曰：「臣家相傳之尺，乃舜時同度之尺」 也，乃以其尺為之度。諸侯聞之，爭召班。然班亦本木 工之聖者也。

世儒有言，學樂必先等字。若然，《三百篇》無一章中律 者。經言律和聲，未聞以律就聲也。夫人之聲，有洪者、 細者、亮者，萬萬不齊。古之聖人，雖堯、舜之聲，亦不能 合律，惟大禹一人，聲可為律耳。正使人人之聲皆中 律，亦只五聲，人有八十四喉舌。且如「呦呦鹿鳴」一句， 上「呦」字宮，下「呦」字徵，豈一字二音哉？協以就律耳。等 字雲者，非知樂者之言也。先儒之論律呂，正聲倍子 而為母，子聲半正而為子。若黃鐘之管，正聲九寸為 均，其子聲則四寸半。三分損一，下生林鐘之子；又三 分益一，上生太簇之子。由是第之，終於中呂，以從十 二母相生之法。故黃鐘為宮，而下生林鐘為徵；林鐘 上生太簇為商，太簇下生南呂為羽，「南呂上生姑洗 為角」，此黃鐘之調，皆得三分之次，故用《正律》之聲。大 呂為宮而下生夷則為徵，夷則上生夾鐘為商，夾鐘 下生無射為羽，無射上生中呂為角。此大呂之調，皆 得三分之次，故用《正律》之聲。「太簇為宮而下生南呂 為徵，南呂上生姑洗為商，姑洗下生應鐘為羽，應鐘 上生蕤賓為角。」此太簇之調，皆得三分之次，故用正 律之聲，夾鐘為宮，而下生無射為徵；無射上生中呂 為商，中呂上生黃鐘為羽。黃鐘正律聲長，非中呂三 分去一之次，故用子聲為羽。黃鐘下生林鐘為角，林 鐘子律聲短，非中呂為商之次，故還用正聲為角。此 夾鐘之調，正聲四，子聲一也。姑洗為宮，而下生應鐘 為徵，應鐘上生蕤賓為商，蕤賓上生大呂為羽。大呂 正律聲非蕤賓三分去一之次，故用子聲為羽。大呂 下生夷則為角，夷則子律聲短，非蕤賓為商之次，故 還用正聲為角。此姑洗之調，正聲四，子聲一也。中呂 為宮而上生黃鐘為徵。黃鐘正律聲長，非中呂三分 去一之次，故用子聲為徵。黃鐘下生林鐘為商。林鐘 子律聲短，非中呂為宮之次，故還用正聲為商。林鐘 上生太簇為羽，太簇正律聲長，非林鐘三分去一之 次，故用子聲為羽。太簇下生南呂為角。此中呂之調， 正聲三，子聲二也。蕤賓為宮而上生大呂為徵。大呂 正律聲長，非蕤賓三分去一之次，故用子聲為徵。大 呂下生夷則為商，夷則上生夾鐘為羽。夾鐘正律聲 長，非夷則三分去一之次，故用子聲為羽。夾鐘下生 無射為角，無射子律聲短，非夷則為商之次，故還用 正聲為角。此蕤賓之調，正聲三，子聲二也。林鐘為宮， 而上生太簇為徵。太簇正律聲長，非林鐘三分去一 之次，故用子聲為徵。太簇下生南呂為商，南呂上生 姑洗為羽。姑洗正律聲長，非南呂三分去一之次，故 用子聲為羽。姑洗下生應鐘為角，應鐘子律聲短，非 南呂為商之次，故還用正聲為角。此《林鐘》之調，正聲 三，子聲二也。夷則為宮，而上生夾鐘為徵。夾鐘正律 聲長，非夷則三分去一之次，故用子聲為徵。夾鐘下 生無射為商。無射子律聲短，非夷則為宮之次，故還 用正聲為商。無射上生中呂為羽，中呂正律聲長，非 無射三分去一之次，故用子聲為羽。中呂上生黃鐘 為角，黃鐘正律聲長，非無射為商之次，故用子聲為 角。此夷則之調，正聲二，子聲三也。南呂為宮，南呂上 生姑洗為徵。姑洗正律聲長，非南呂三分去一之次， 故用子聲為徵。姑洗下生應鐘為商。應鐘子律聲短， 非南呂為宮之次，故用正聲為商。應鐘上生蕤賓為 羽，蕤賓正律聲長，非應鐘三分去一之次，故用子聲 為羽。蕤賓上生大呂為角。大呂正律聲長，非應鐘為 商之次，故用子聲為角。此南呂之調，正聲二，子聲三 也。無射為宮而上生中呂為徵，中呂正律聲長，非無 射三分去一之次，故用子聲為徵。中呂上生黃鐘為 商，黃鐘正律聲長，非無射為宮之次，故用子聲為商。 黃鐘下生林鐘為羽，林鐘正律聲長，非黃鐘子聲三 分去一之次，故用子聲為羽。林鐘上生太簇為角，太 簇正律聲長，非黃鐘子聲為商之次，故用子聲為角。 此無射之調，正聲一，子聲四也。應鐘為宮，應鐘上生 蕤賓為徵。蕤賓正律聲長，非應鐘三分去一之次，故 用子聲為徵。蕤賓上生大呂為商。大呂正律聲長，非 應鐘為宮之次，故用子聲為商。大呂下生夷則為羽， 《夷則》正律聲長，非蕤賓子聲為徵之次，故用子聲為 羽。夷則上生夾鐘為角，夾鐘正律聲長，非大呂子聲 為商之次，故用子聲為角。此應鐘之調，正聲一，子聲四也。凡此蔽於十二律均旋為宮之說，失《周禮》「三宮」 之意也。三宮旋相而唱和有應，曷嘗有子聲邪？若以 為十二律皆有子聲，然則黃鐘、大呂、太簇三律，何獨 止用正聲邪？

律呂直解

《黃鐘第一解》曰：「此黃鐘之體數也。十分為寸，分釐、毫絲並同斷用之，九以為十。何以十？自然之數也。」

長九寸，空圍九分，積八百一十分。

解曰：「從長九寸，寸者十分」 ，黃鐘之長通有九寸也。空圍九分，分者十分寸之一，黃鐘之管滿於圍中，容九方分也。積實八十一分，黃鐘之管從長九寸，寸十分，黃鐘九十分空，圍中九分。每長一分，圍必九分，以九十因之，則八百一十分也。

黃鐘分寸圖

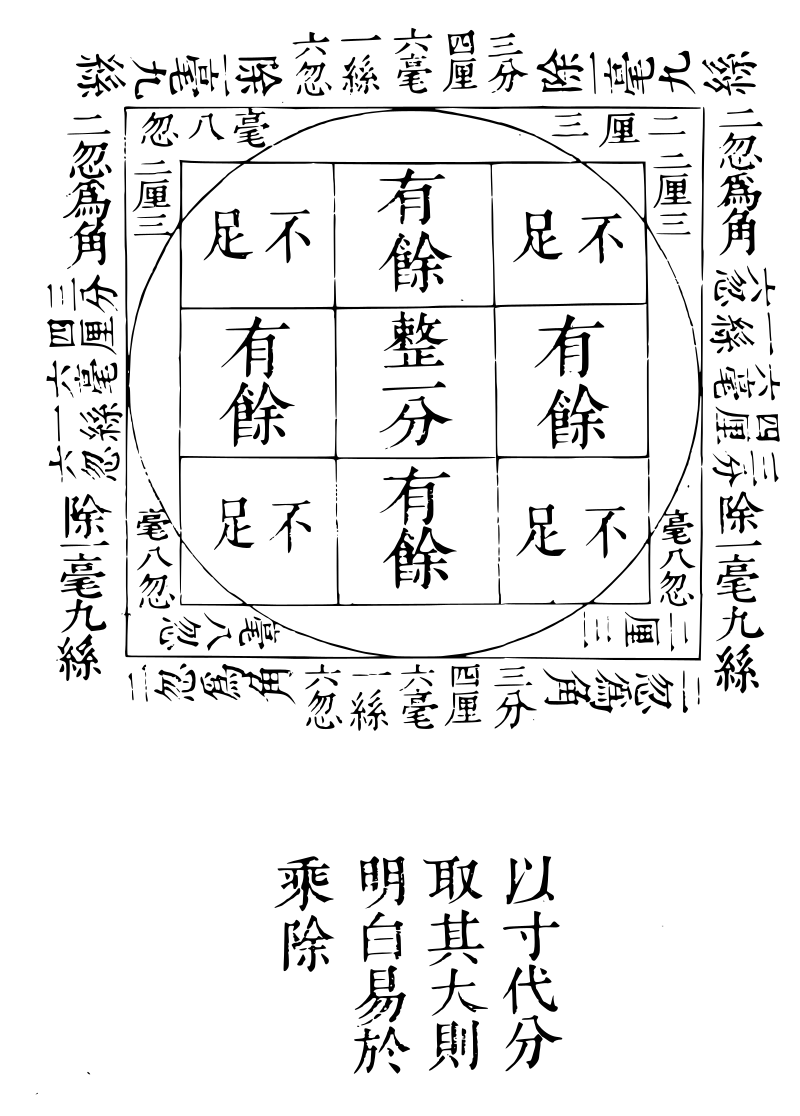
員田術：三分益一，得十二分。

解曰：「三分為一分，三分，九分也。又益一分，共四分十二分也。以九方分平置，又三分益一分，共十二方分。」

以《開方法》除之。

《解》曰：以上一分分割為四片，每片二釐五毫，貼於九方分四面，又每片除一毫九絲二忽為角，每片上得二釐三毫八忽。

得三分四釐六毫強，為實徑之數。

解曰：「中九方分四面各得三分，外四面各二釐三毫八忽，東與西四釐六毫一絲六忽，南與北亦然。是其縱橫又得三分四釐六毫一絲六忽，為實徑之數。」

不盡三毫八絲四忽。

解曰：此補四角之數也。本以一分割作四片，每片二釐五毫，兩面該五釐合九方分該三分五釐徑。今每片取一毫九絲二忽補角兩面該三毫八絲四忽徑，止得三分四釐六毫一絲六忽，猶餘三毫八絲四忽也。

今求圓積之數。

解曰：「謂圍圓之數並內積之數也。」

以徑三分四釐六毫自相乘。

《解》曰：「不用一絲六忽，每一分得三分四釐六毫，每一釐得三釐四毫六絲，每一毫得三毫四絲六忽。」〈分以三乘，釐以四乘，毫以六乘。〉

得十一分九釐七毫一絲六忽。

解曰：若用一絲六忽時，正十二方分，惟不用一絲六忽，故止得如此。以上所乘計之，分之所得者，十分三釐八毫；釐之所得者，一分三釐八毫四絲；毫之所得者，二釐六絲十六忽。總計所得，十一方分零九釐七毫一絲六忽。

加以開方不盡之數，二毫八絲四忽。

解曰：「此不盡之數，與上不同。上不盡之數乃是以三分四釐六毫一絲六忽為徑，不盡三毫八絲四忽除去，補四角成十二方分。此不盡之數乃是以三分四釐六毫為徑，於十二方分中，餘得此數。」

得一十二分。

《解》曰：「以十一分九釐七毫一絲六忽，合二毫八絲四忽，共得十二方分，如前開方之數。」

以管長九十分乘之，得一千八十分，為《方積》之數。

《解》曰：「每管一分，該十二分，積九十分而計之，共一千八十分為方積之數。徑三分四釐六毫一絲六忽，周方共十三分八釐四毫六絲四忽。」

四分取三，為《圓積》之數，得八百一十分。

解曰：「以一千八十分作四分，則一分該二百七十分。四分中取三分，為圓積之數，該八百一十分。以九方分積中計之，徑三分四釐六毫一絲六忽，周圓十分八釐三毫四絲八小忽○八秒。」〈蔡十分三釐八毫則少，彭「十分八釐七毫則多。」 〉

彭氏曰：「黃鐘律管有從長，有面羃，有空圍，有周，有徑， 有積實。」

解曰：「從長」 者，只以黃鐘管上下言之，不以積論也。一一管二九寸三九十分，四九百釐五九千毫六九萬絲。面羃者，上論黃鐘管面上中郛之數也。空。

圍者，論圍圓中所容之數，合面羃積實之數也。以方分計之，一分整四分有餘，四分不足，以有餘補不足。每長一分，當有九方分充滿於黃鐘之管。《周廣》者，九方分之郛，黃鐘管周圓之數也，當有十分八釐三毫四絲零八小忽○八秒。「徑」 者，論黃鐘管直徑之數也。以管三分得一，當有三分四釐六毫一絲六忽。「內積」 者，論黃鐘管上下空圍中之數也。七九為絲法，八九十為毫法，九九百為釐法，十九千為分法，十一九萬為寸法，十二、八十一萬為黃鐘之實。通計黃鐘之實，一管九寸，九十分乘空圍九分，八百一十分，八十一萬釐，八萬萬一千萬毫，八千萬萬一百萬萬絲。

積黍：

解曰：「一為一分，黃鐘之管長九十分，立九十黍，每一分空，圍中可容十三黍。又三分黍之一，以九十因之，可容千二百黍矣。夫黃鐘之管，一黍為一分，黃鐘之實止八百一十方分，何以能容千二百黍哉？蓋方與圓不同，方無空，圓有空，以圓頂對圓頂，則一為一分。若縱橫補塞，其空充滿於黃鐘之管，可容千二百黍。」 九十分之，則每分該十三黍又三分黍之一矣。用羊頭山黍以篩子篩之，去其大者、小者而用中者。若管既定，則隨大小之宜而實其數，尤為至當。

《黃鐘之實第二解》曰：「此黃鐘之用數也。九分為寸，分釐毫絲並同，約體之十以為九。何以九因三分損益而立也。若以十則三分不盡其數，必有餘剩之數，且難推算。約之為九，既不失其十之長，又無餘剩之數，易於推筭矣。又置一而三，三住而九間之，亦理之自然也。」

子：一，　黃鐘之律。

解曰：「此黃鐘通長之管也，一而已。太極以一含三，此一管含下文寸分釐毫絲之法數，實十一箇三也。置一也，陽辰之始也。」

丑三　「為絲法。」

解曰：「黃鐘之數起於絲，然空圍中九分，八面相乘各三分，每一絲必有三絲，故三為一絲。由一而三加為三三箇一也。此雖由一而三，然陰陽各為一事，不相涉焉。第一三也，陰辰之始也。」

寅九　為寸數。

《解》曰：「此黃鐘之九寸也。一管九寸，與上寸為一，連事由三而三加為九三箇三也，第二三也，一寸含三寸。」

卯二十七　為毫法

《解》曰：「黃鐘之數，九絲為毫，然一毫乘圍，必有三毫，故九三二十七為一毫也。與上丑為一連事由九而三加為二十七，三箇九也，第三三也。」

辰八十一　為分數。

解曰：「此黃鐘八十一分也，一寸、九分九寸共八十一分，與上寅為一連事由二十七而三加為八十一，三箇二十七也，第四三也，一分含三分。」

巳：二百四十三　為釐法。

《解》曰：「黃鐘之數，九毫為釐，然一釐乘圍，必有三釐二十七。」 既為一毫，則九箇二十七該一百四十三為一釐也。與上卯為一連，事由八十一而三加為二百四十三，三箇八十一也，第五三也。

午七百二十九　為釐數。

《解》曰：「此黃鐘七百二十九釐一分，九釐八十一分，共該七百二十九釐，與上辰為一連事由二百四十三而三加為七百二十九，三箇二百四十三也，第六三也，一釐含三釐。」

未二千一百八十七，　為分法。

解曰：「黃鐘之數，九釐為分，然一分乘圍，必有三分」 二百四十三既為一釐，則九箇二百四十三該二千一百八十七為一分也。與上已為一連，事由七百二十九而三加為二千一百八十七，三箇七百二十九也。第七，三也。

申：六千五百六十一，　為毫數。

《解》曰：「此黃鐘之六千五百六十一毫也。一釐九毫七百二十九釐，共該六千五百六十一毫，與上午為一連事由二千一百八十七而三加為六千五百六十一，三箇二千一百八十七也。第八三也，一毫含三毫也。」

酉一萬九千六百八十三，　為「寸法。」

解曰：「黃鐘之數，九分為寸」 ，然一寸乘圍必有三寸。二千一百八十七既為一分，則九箇二千一百八十七該一萬九千六百八十三為一寸也。與上未為一連，事由六千五百六十一而三加為一萬九千六百八十三，三箇六千五百六十一也。第九三也。所謂「九三之為寸法」 是也。

戌五萬九千四十九，　為「絲數。」

《解》曰：「此黃鐘之五萬九千四十九絲也，一毫九絲。」

六千五百六十一毫，共該五萬九千四十九也，與上申為一連事由一萬九千六百八十三而三加為五萬九千四十九，三箇一萬九千六百八十三也，第十三也，「一絲含三絲。」

亥：十七萬七千一百四十七，　為黃鐘之實。

解曰：黃鐘之數，九寸為管。然乘圍而三之，一萬九千六百八十三。既為一寸，則九箇一萬九千六百八十三，該十七萬七千一百四十七為九寸一管，黃鐘之實也。與上酉為一，連事由五萬九千四十九而三加為十七萬七千一百四十七，三箇五萬九千四十九也。第十一三也。所謂「置一而十一三之，為黃鐘之實」 是也。

子寅辰午申戌六陽辰，

《解》曰：「以六律在位故也。子丑、寅、卯、辰、巳則正陽。」

亥酉未巳卯丑六陰辰。

解曰：以六呂在位故也。午未、申酉、戌、亥，則正陰，黃鐘生十一律。第三解曰：「十二律相生亦在內。」

黃鐘管圖

子：一分　一為九寸。

解曰：子，黃鐘也。一黃鐘之管也。下十一律皆由此管而生　。本註者，黃鐘生十一律也。圈外註者，十二律三分，損益相生也。

林鐘管圖

丑三分二　一為三寸。

《解》曰：「丑，林鐘也。三分三分乎子也。」 二，林鐘之管也。以黃鐘九寸，分為三分，每分三寸，得其二分，計六寸，為林鐘之數也。

分黃鐘九寸為三分，去一分下生《林鐘》，得二分，計六寸。

太蔟管圖

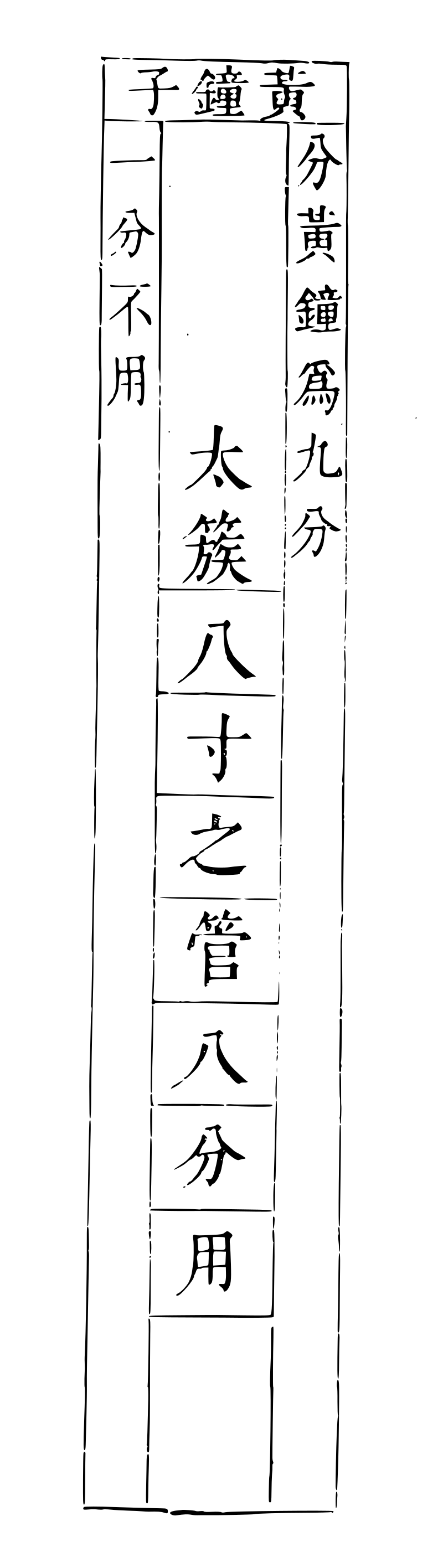
寅：九分八　一為一寸。

解曰：「寅，太蔟也。九分九分乎子也。八，太蔟之管也。」 以黃鐘九寸，分為九分，每分一寸，得其八分，計八寸，為太蔟之數也。

分《林鐘》六寸為三分，每分二寸，益一分，上生太蔟，得四分，計八寸。

南呂管圖

卯二十七分十六，　三為一寸，　一為三分。

《解》曰：「卯，南呂也，二十七分。二十七分乎子也。十六，南呂之管也。」 以黃鐘九寸分為二十七分，每三分一寸，得其十六分，計五寸三分，為南呂之數也。分太蔟八寸為三分，每分二寸六分，去一分下生南呂，得二分，計五寸三分。

姑洗管圖

辰八十一分六十四，　九為一寸，　一為一分。

《解》曰：「辰，姑洗也，八十一分，八十一分乎子也。六十四，姑洗之管也。」 以黃鐘九寸分為八十一分，每九分一寸，得六十四分，計七寸一分，為姑洗之數也。分南呂五寸三分為三分，每分一寸七分，益一分上生太蔟，得四分，計七寸一分。

應鐘管圖

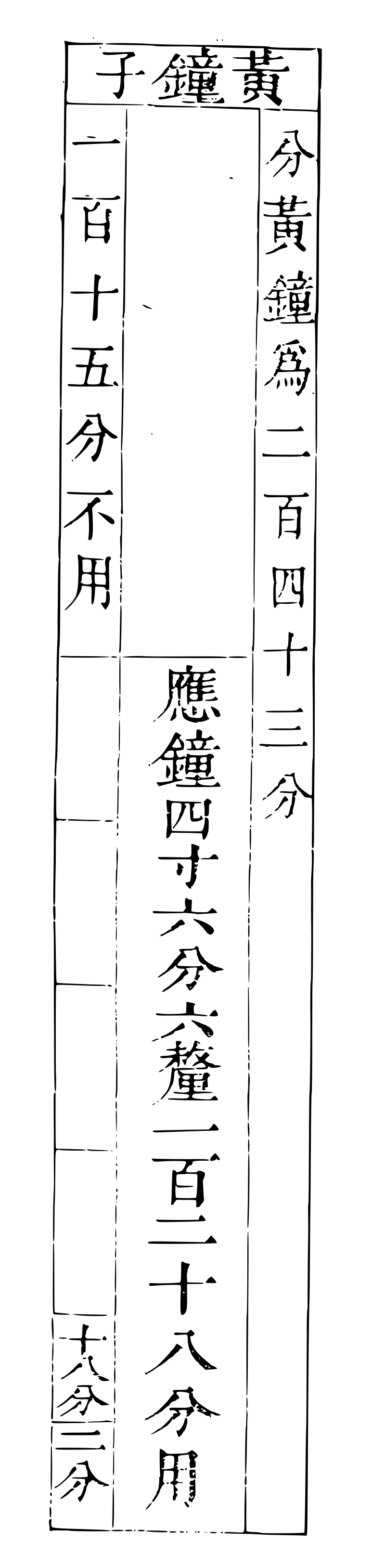
巳：二百四十三分，一百二十八，　二十七為一寸， 三為一分，　一為三釐。

《解》曰：「巳，應鐘也，二百四十三分。二百四十三分乎子也，一百二十八應鐘之管也。以黃鐘九寸，分為二百四十三分，每二十七分一寸得一百二十八分，計四寸六分六釐，為應鐘之數也。」

分姑洗七寸一分為三分，每分二寸三分三釐，去一分下生應鐘，得二分，計四寸六分六釐。

蕤賓管圖

午：七百二十九分，五百一十二，　八十一分為一寸。

九為一分　，一為一釐。

《解》曰：「午，蕤賓也，七百二十九分。七百二十九分乎子也。五百一十二，蕤賓之管也。」 以黃鐘九寸分為七百二十九分，每八十一分一寸得五百一十二，計六寸二分八釐，為蕤賓之數也。

分應鐘四寸六分六釐為三分，每分一寸五分二釐，益一分上生《蕤賓》，得四分，計六寸二分八釐。

大呂管圖

未：二千一百八十七分。一千二十四。　二百四十三 為一寸，　二十七為一分，　三為一釐，　一為三毫。

解曰：「未，大呂也，二千一百八十七分。二千一百八十七分乎子也。一千二十四，大呂之半管也。」 以黃鐘九寸分為二千一百八十七分，每二百四十三分一寸，得一千二十四，計四寸一分八釐三毫。在陽倍之，為八寸三分七釐六毫，為大呂之數也。分蕤賓六寸二分八釐為三分，每分二寸八釐六毫，去一分下生大呂，得二分，計四寸一分八釐三。

毫，在陽倍之。通計八寸三分七釐六毫。〈在陽謂居五也〉

夷則管圖

申，六千五百六十一分四千九十六。　七百二十九 為一寸，　八十一為一分，　九為一釐，　一為一毫。

解曰：「申，夷則也，六千五百六十一分。六千五百六十一分乎子也。四千九十六，夷則之管也。」 以黃鐘九寸，分為六千五百六十一分，每七百二十九分一寸，得四千九十六，計五寸五分五釐一毫，為夷則之數也。

分大呂四寸一分八釐三毫，為三分。每分一寸三分五釐七毫，益一分上生《夷則》，得四分，計五寸五分五釐一毫。

夾鐘管圖

《酉》，一萬九千六百八十三分八千一百九十二。　二 千一百八十七為寸，　二百四十三為一分，　二十 七為一釐，　三為一毫，　一為二絲。

《解》曰：「酉，夾鐘也，一萬九千六百八十三分。一萬九千六百八十三分乎子也，八千一百九十二，夾鐘之半管也。以黃鐘九寸分為一萬九千六百八十三分，每二千一百八十七為一寸，得八千一百九十二，計三寸六分六釐三毫六絲，在陽倍之，共七寸四分三釐七毫三絲，為夾鐘之數也。」

分《夷則》五寸五分五釐一毫為三分，每分一寸七分七釐六毫三絲，去一分下生夾鐘，得二分，計三寸六分六釐三毫六絲，在陽倍之，通計七寸四分三釐七毫三絲也。〈「在陽」 ，謂居卯也。〉

無射管圖

戌，五萬九千四十九分。三萬二千七百六十八。　六 千五百六十一為一寸，　七百二十九為一分，　八 十一為一釐，　九為一毫，　一為一絲。

《解》曰：「戌，無射也，五萬九千四十九分。五萬九千四十九分乎子也。三萬二千七百六十八，無射之管也。以黃鐘九寸，分為五萬九千四十九分，每六千五百六十一為一寸，得三萬二千七百六十八，計四寸八分八釐四毫八絲，為無射之數也。」

分夾鐘三寸六分六釐三毫六絲為三分，每分一

寸二分二釐一毫二絲。益一分上生無射，得四分，計四寸八分八釐四毫八絲。

仲呂管圖

亥，一十七萬七千一百四十七分。六萬五千五百三 十六，一萬九千六百八十三為一寸，　二千一百八 十七為一分，　二百四十三為一釐，　二十七為一 毫，　三為一絲，　一為一忽。

《解》曰：「亥，仲呂也。十七萬七千一百四十七分。十七萬七千一百四十七分乎子也。六萬五千五百三十六，仲呂之半管也。以黃鐘九寸，分為十七萬七千一百四十七分，每一萬九千六百八十三為一寸，得六萬五千五百三十六，計三寸二分八釐六毫二絲三忽，在陽倍之，共六寸五分八釐三毫四絲六忽，為仲呂」 之數也。

分無射四寸八分八釐四毫八絲，為三分。每分一寸五分八釐七毫五絲六忽，去一分下生仲呂，得二分，計三寸二分八釐六毫二絲三忽，在《陽》倍之六寸五分八釐三毫四絲六忽。〈「在陽」 ，謂居巳也。〉《十二律之實第四解》曰：「十二律各得於黃鐘之數也。」

子黃鐘十七萬七千一百四十七，　全九寸。

解曰：「黃鐘之數，一萬九千六百八十三為一寸，積之則九箇一萬九千六百八十三為九寸，共該十七萬七千一百四十七分。」

《半無》。

一、以十七萬七千一百四十七之數不可分。解曰：一十七萬七千一百四十七分作兩分，一分得八萬八千五百七十三，兩分不得均平，故不可分而無半也。

一以三分損益，上下相生之所不及，故「亦無所用也。」

解曰：「黃鐘不為他律所役，故損益不及，損益不及，故不用半。如林鐘受損於黃鐘三分九寸，林鐘得二分六寸一分三寸為半，非半無以成其數也。如太簇受益於林鐘三分六寸，太簇得四分八寸二分四寸為半，非半亦無以成其數也。獨黃鐘不然。」

「丑」，林鐘十一萬八千九十八　全，六寸　半，三寸不 用。

解曰：「凡律用半者，以上律短而下律長，或均或短，不及數，故下律用半，以成宮、商、角、徵、羽之五聲。林鐘、南呂、應鐘三律，受役於黃鐘、太簇，為徵、羽。其上太簇、姑洗、蕤賓，皆本然多寡之數。其餘為宮、商、角，皆依序而下，乃自為上律。而上律更無短者，而半又將何所用哉？」

寅太簇十五萬七千四百六十四　全八寸　半四。

寸

卯南呂十萬四千九百七十六　全五寸三分　半。

二寸六分不用

解曰：「黃鐘之數二千一百八十七為一分。積而三之，六千五百六十一為三分。五寸，得九萬八千四百一十五。合三分之數，共十萬四千九百七十六。」

辰姑洗十三萬九千九百六十八　全七寸一分 半三寸五分。

巳應鐘九萬三千三百一十二　全四寸六分六釐。

半，二寸三分三釐不用。

解曰：「黃鐘之數，二百四十三為一釐。積而六之，一千四百五十八為六釐。四寸六分，得九萬一千八百五十四。合六釐之數，共九萬三千三百一十二。」

午蕤賓十二萬四千四百一十六　全六寸二分八 釐　半三寸一分四釐。

未大呂十六萬五千八百八十八。　全八寸三分七 釐六毫，　半四寸一分八釐三毫。

《解》曰：「黃鐘之數，二十七為一毫。積而六之，一百六十二為六毫八寸三分七釐，得十六萬五千七百二十六。合六毫之數，共十六萬五千八百八十八。」

《申夷則》，十一萬五百九十二，　全五寸五分五釐一毫，　半二寸七分二釐五毫。

酉夾鐘十四萬七千四百五十六　全七寸四分三 釐七毫三絲，　半三寸六分六釐三毫六絲。

《解》曰：「黃鐘之數三為一絲，積而三之，為九七寸四分三釐七毫，得十四萬七千四百四十七，合二絲之數，共十四萬七千四百五十六。」

戌，無射九萬八千三百四　全四寸八分八釐四毫 八絲　半二寸四分四釐二毫四絲。

「亥仲呂」十三萬一千七十二　全六寸五分八釐三 毫四絲六忽。〈餘二算〉半三寸二分八釐六毫二絲三忽。

解曰：黃鐘之數，一為三忽，積而六之為二，六寸五分八釐三毫四絲，得十三萬一千七十，合六忽之數，共十三萬一千七十二　。數至仲呂不生。解曰：「數止於仲呂，十二不生者何也？蓋律呂相生，以三分損益。至於仲呂，寸分釐毫絲忽，雖可三分，數十三萬一千七十二，並半數三分亦不足，故不以相生也。」〈「二算」 者，三《忽》為「一」 也。〉

寸忽可三分

二寸一分八釐七毫一絲五忽。〈以「三忽」 為絲，算亦同。〉

全　　二寸一分八釐七毫一絲五忽；〈但為一絲三忽〉

二寸一分八釐七毫一絲五忽。

一寸八釐八毫七忽

半　　一寸八釐八毫七忽。

一寸八釐八毫七忽

數不可三分

一十三萬一千七十二

四　　三　　六　　、《九　　　一》

全，　四　萬三　千六　百九　十　　　　；餘，二。

四　　三　　《六　　九》。

六萬五千五百三十六

二　　一　　八　　、《四　　五一》。

半，　二　萬一　千八　百四　十五　　　；餘一。

二　　一　　八　　、四　　五

《變律第五解》曰：「變律者，在正律之位，而非正律之聲也。然律所以有變者，其故有三：其一黃鐘至尊為君，不為他律役，而每一律皆當為五聲。二變共七聲，如黃鐘為宮，則得其正矣。其為無射之商、夷則之角、蕤賓之變徵、仲呂之徵、夾鐘之羽，大呂之變宮，皆受役於他律，故皆當變。黃鐘既變其次所生之律，若仍本」律，則長不成曲，亦當變焉。如黃鐘為商，則太簇之角、姑洗之變徵、林鐘之羽、南呂之變宮，皆隨而變。如黃鐘為角，則太簇之變徵、林鐘之變宮，皆隨其變。如為徵，則應鐘為變徵，為羽，則太簇為變宮。臣之從君，理固然也。其二，以黃鐘、林鐘、太簇、南呂、姑洗、應鐘上六律長，蕤賓、大呂、夷則、夾鐘、無射、仲呂下六律短。以上律役下律，則或正或半，通而和；以下律役上律，則或正或半，戾而不和。故以上律役上律，以下律役下律，以上律役下律，皆不必變。惟以下律役上律，則必變其上律，使少短，而與下律適也。其三相生之法，至仲呂而窮，使再生六律，則上律獨不能遍七聲之用，下律亦無由而通。故以六三之七百二十九，因仲呂之實十三萬一千七十二，三分而益之，再得六律，以為變也。其實乃仲呂之實相乘三分益一，再生黃鐘，不及舊數，止得十七萬四千七百六十二。其下相因而生五律，莫不於舊為減。是皆數之自然，而非人力私智增損其間以求合乎音韻也。其所以變有六者，以數至「應鐘而窮，然至此則十二律七聲循環相役以遍」，莫非天然自有也。律呂之數妙矣哉！〈其實止為律，至《仲律》而窮，不足旋宮之用。〉

黃鐘，十七萬四千七百六十二。〈小分四百八十六〉 全八寸七分八釐一毫六絲二忽，不用。

半四寸三分八釐五毫三絲一忽。

《解》曰：「仲呂之實十三萬一千七十二，以三分之不盡，二筭當有以通之。律當變者有六，故置一而六三之，得七百二十九、七百二十九。因仲呂之十三萬一千七十二，每仲呂之一當七百二十九，共九千五百五十五萬一千四百八十八。以三分之，每分得三千一百八十五萬四百九十六，又益一分，上生黃鐘，共一」 萬二千七百四十萬一千九百八十四。復以七百二十九歸之，為十七萬四千七百六十二箇七百二十九零四百八十六。每黃鐘之一，當七百二十九，為黃鐘十七萬四千七百六十二零三分一之二。以寸法計之十五萬七千四百六十四，得寸者八；以分法計之一萬五千三百九，得分者十；以釐法計之一千九百四十四，得釐者八。以毫法計之二十七，得毫者一。以絲法計之一十八，得絲者六。七百二十九為一一。小分七百二十九為三，得三分一之二為四百八十六，為二忽。積而計之，為十七萬四千七百六十二。小分四百八十六半四寸三分八釐五毫三絲一忽，得八萬。

七千三百八十一，小分二百四十三。不用全者，所受役之律，無長於此者也。下同。且黃鐘君也。

林鐘十一萬六千五百八。〈小分三百二十四〉

全五寸八分二釐四毫一絲一忽三初；

半二寸八分五釐六毫五絲六初。

《解》曰：「以黃鐘一萬二千七百四十萬一千九百八十四，三分之，每分得四千二百四十六萬七千三百二十八，損一分下生林鐘八千四百九十三萬四千六百五十六」 ，以七百二十九歸之，為林鐘之十一萬六千五百八箇七百二十九零三百二十四。八十一，為一初。

太簇，十五萬五千三百四十四。〈小分四百三十二〉 全七寸八分二毫四絲四忽七初不用；

半三寸八分四釐五毫六絲六忽八初。

解曰：「以林鐘八千四百九十三萬四千六百五十六，三分之，每分得二千八百三十一萬一千五百五十二，益一分上生太簇一萬一千三百二十四萬六千二百八，以七百二十九歸之，為太簇之十五萬五千三百四十四箇七百二十九零四百二十二。」

南呂，十萬三千五百六十三。〈小分四十五〉

《全》五寸二分三釐一毫六絲一初六秒。

半二寸五分六釐七絲四忽五初二秒。

《解》曰：「以太簇一萬一千三百二十四萬六千二百八三分之，每分得三千七百七十四萬八千七百三十六，損一分下生南呂七千五百四十九萬七千四百七十二，以七百二十九歸之，為南呂之十萬三千五百六十三箇七百二十九零四十五。」

姑洗，十三萬八千八十四。〈小分六十〉

全七寸一釐二毫二絲一初二秒不用。

半三寸四分五釐一毫一絲一初一秒。

《解》曰：「以南呂七千五百四十九萬七千四百七十二，三分之，每分得二千五百十六萬五千八百二十四，益一分上生姑洗一萬六十六萬三千二百九十六，以七百二十九歸之，為姑洗之十三萬八千八十四箇七百二十九零六十。」

應鐘九萬二千五十六。〈小分四十〉

全四寸六分七毫四絲三忽一初四秒；〈餘算〉

半二寸三分三毫六絲六忽六秒強，不用。

《解》曰：「以姑洗一萬六十六萬三千二百九十六，三分之，每分得三千三百五十五萬四千四百三十二，損一分下生應鐘六千七百十萬八千八百六十四，以七百二十九歸之，為應鐘之九萬二千五百六箇七百二十九零四十。」

應鐘六千七百十萬八千八百六十四，三分之不盡一算。

二　二　三　六，　九　六　二　一。

二千二百三十六萬九千六百二十一。〈不盡一算〉 二　二　三　六　九　六　二。